Continuamos con esta serie de post para ayudar comprender mejor qué significa la toma de decisiones en ciencias sociales. Tras explorar diversos fenómenos no lineales y caóticos, ahora toca el turno de comprender la diferencia entre un fenómeno completamente determinista y uno totalmente aleatorio. Aunque en rigor ninguno de los casos que vamos a comentar aquí son complemente deterministas o totalmente aleatorios, sí que nos sirven como una buena aproximación para ilustrar que en ambos casos se pueden realizar predicciones.
Como siempre, vamos a ayudarnos de Maxima para la visualización, y en este post también voy a mostrar códigos de C para estimular el aprendizaje de los estudiantes de marketing que quieran realizar sus propias simulaciones.
Ecuación determinista
Sin entrar en matices, podemos entender que una ecuación es determinista cuando al conocer las variables independientes somos capaces de predecir exactamente la variable dependiente. Es común que ciertas leyes físicas se puedan representar por ecuaciones completamente deterministas, como la Segunda Ley de Newton
Dado que a es la aceleración de la gravedad (que tomaremos como constate de valor 9.81 m/s2), cuando se conoce la masa de un objeto en caída libre se puede calcular la fuerza con la que es atraído por la Tierra.
A continuación muestro un código en C que calcula el valor de la fuerza para valores de la masa de 1 a 10.
| #include <stdio.h> #include <stdlib.h> #define a 9.81 #define n 10 double Fuerza(m) { double f; f=m*a; return f; } int main() { int m; FILE*fout; fout=fopen(“Datos.dat”, “w”); for(m=1;m<=n;m++) { fuerza(m); printf(“%d\t %f\n”,m,Fuerza(m)); fprintf(fout, “%d\t %f\n”,m,Fuerza(m)); } fclose(fout); return 0; } |
Lo que hace este programa es crear una función llamada “Fuerza” con el argumento de la masa “m”. Después, creamos un bucle con los 10 primeros valores enteros de m, por el cual para cada uno de esos valores se llame a la función “Fuerza(m)”, y se calcule su resultados. Esos resultados se muestran en pantalla “printf” y también en un archivo denominado “Datos.dat”, donde quedan regristrados los valores de la masa y de la fuerza.
Ese arcivho “Datos.dat” puede llevarse a Excel o a cualquier otro programa para su representación gráfica.
Lo que vamos a hacer ahora es realizar la misma programación, pero esta ve en wxMaxima, adjuntando el gráfico correspondiente:
| Fuerza(m,a):=block([m_list, f_list], m_list: makelist(m,m,1,10,1), f_list:m_list*a, return(f_list))$ plot2d([[discrete, Fuerza(m,9.81), m_list],[discrete, Fuerza(m,9.81), m_list]], [x,0,10],[y,0,100], [style, points, lines],[color, red, green], [xlabel, “masa (kg)”],[ylabel, “Fuerza (N)”], [legend, false]); |
En este caso hemos definido la función “Fuerza” con dos argumentos (m,a), es decir, la masa y la aceleración. Como paso intermedio hemos creado las variables locales con el listado de valores de la masa (m_list) de 1 a 10, y con el de la fuerza (f_list). Cuando se llama a la función desde plot2d, sólo hay que proveer del argumento que falta (la aceleración) y representar esos puntos discretos, unidos por una recta.
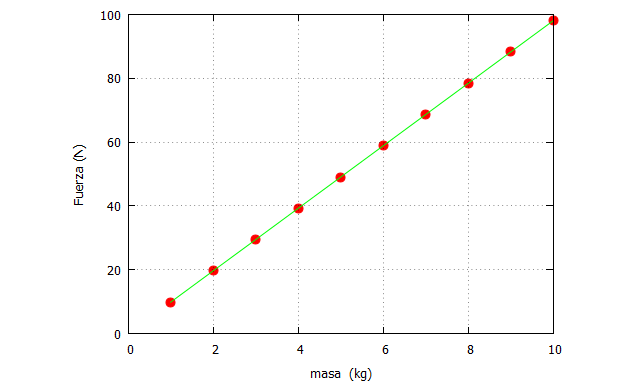
Podemos ahora escribir un nuevo programa para que los usuarios indiquen los valores de la masa “a mano”, es decir, un programa que pregunte por línea de comandos cuáles son los valores de la diferentes masas, y que luega devuelva las correspondientes fuerzas. El código (realizado para 5 observaciones de entrada) es el siguiente:
| #include <stdio.h> #include <stdlib.h> #define a 9.81 #define n 5 double fuerza(m) { double f; f=m*a; return f; } int main() {int i; int m[n]; FILE*fout; fout=fopen(“Datos2.dat”, “w”); printf(“Indica la masa 1\n”); scanf(“%d”, &m[0]); fuerza(m[0]); printf(“Indica la masa 2\n”); scanf(“%d”, &m[1]); fuerza(m[1]); printf(“Indica la masa 3\n”); scanf(“%d”, &m[2]); fuerza(m[2]); printf(“Indica la masa 4\n”); scanf(“%d”, &m[3]); fuerza(m[3]); printf(“Indica la masa 5\n”); scanf(“%d”, &m[4]); fuerza(m[4]); printf(“Fuerzas generadas\n”); printf(“%d\t%f\n%d\t%f\n%d\t%f\n%d\t%f\n%d\t%f\n”, m[0],fuerza(m[0]),m[1],fuerza(m[1]), m[2],fuerza(m[2]),m[3],fuerza(m[3]),m[4],fuerza(m[4])); fprintf(fout, “%d\t%f\n%d\t%f\n%d\t%f\n%d\t%f\n%d\t%f\n” ,m[0],fuerza(m[0]),m[1],fuerza(m[1]), m[2],fuerza(m[2]),m[3],fuerza(m[3]),m[4],fuerza(m[4])); fclose(fout); return 0; } |
Así, por línea de comandos se pueden indicar 5 valores de la masa, que en este caso de ejemplo han sido 8, 3, 1, 6 y 10:

Esos datos se han guardado en el artivo “Datos2.dat”, que puede llevarse de nuevo a cualquier software “más amigable”.
En wxMaxima vamos a hacer exactamente lo mismo, introduciendo manualmente los valores de la masa como un array de datos. Así, hemos creado un vector de masas “vector_masas”, donde dentro de sus corchetes indicamos cada observación. Luego multiplicamos ese vector por la constante de gravitación universal, lo que nos proporciona la “Fuerza”.
| vector_masas:[8, 3, 1, 6 ,10]$ a:9.81$ Fuerza:vector_masas*a$ plot2d([[discrete, vector_masas, Fuerza], [discrete, vector_masas, Fuerza]], [x,0,10],[y,0,100], [style, points, lines], [color, red,green], [xlabel, “masa (kg)”],[ylabel, “Fuerza (N)”], [legend, false]); |
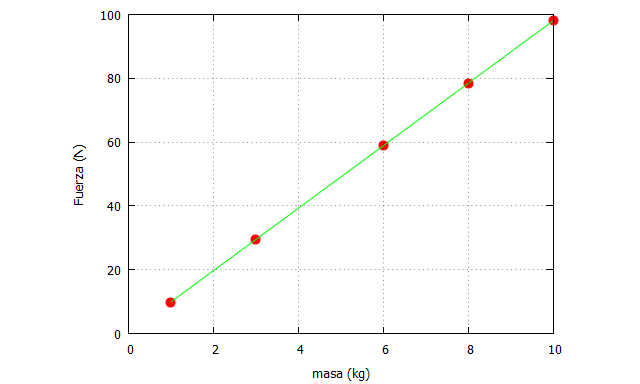
En resumen, podemos realizar las simulaciones que queramos, pero siempre obtendremos una predicción exacta de la Fuerza, ya que conocemos perfectamente sus determinantes. En la práctica, recordemos que no es exactamente así, ya que siempre hay imprecisión en la medida de las variables, y podemos complicar mucho más si consideramos que la aceleración de la gravedad no es constante en todos los puntos del planeta. Pero, como ejemplo sencillo, basta con lo que hemos descrito.
Fenómenos de azar
También podemos realizar predicciones en fenómenos que son aleatorios (o más bien pseudoaleatorios), usando esta vez el lenguaje de la probabilidad. En este caso, no hay determinismo, más bien estamos en el lado opuesto, es decir, no conocemos ninguna variable que influya en el resultado final.
El ejemplo más sencillo es intentar predecir el resultado del lanzamiento de un dado, donde hay 6 resultados posibles: 1,2,3,4,5,6. El código de C que proporciona los valores del espacio muestral y de la probabilidad es el siguiente:
| #include <stdio.h> #include <stdlib.h> #define numdado 6 int main() {int i; double probabilidad; for(i=1;i<=numdado;i++) { probabilidad=(double)1/numdado; printf(“%d\t %f\n”, i, probabilidad); } return 0; } |
En wxMaxima lo podemos programar así:
| numeros_dado:[1,2,3,4,5,6]$ probabilidad:[1/6,1/6,1/6,1/6,1/6,1/6]$ plot2d([[discrete, numeros_dado, probabilidad], [discrete, numeros_dado, probabilidad]], [x,1,6],[y,0,1], [style, points, lines], [color, red,green], [xlabel, “Espacio muestral”],[ylabel, “Probabilidad”], [legend, false]); |
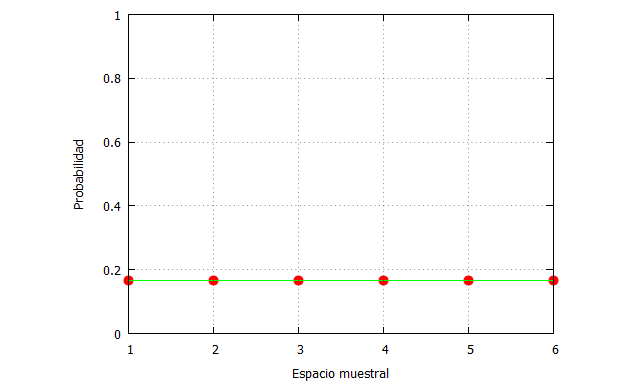
Aunque es una distribución discreta, he dibujado también la línea continua para ilustrar mejor que la probabilidad es la misma, y por tanto, la incertidumbre es máxima. Aquí poco sentido tendría apostar por un número frente a otro; todos tienen la misma probabilidad.
Sin embargo, cuando lanzamos 2 dados la situación cambia. Con el siguiente código de C vamos a generar los 36 valores posibles que se pueden combinar cuando se lanzan dos dados (variaciones con repetación de 6 elementos tomados de dos en dos). Hallamos, de este modo, la suma del resultado de lanzar dos dados.
| #include <stdio.h> #include <stdlib.h> #define numdado 6 int main() {int n, m; int s[n], i, j; for(i=1;i<=numdado;i++) {for(j=1;j<=numdado;j++) {s[n]=i+j;printf(“%d,\t”, s[n]); }} return 0;} |
Esos 36 números generados (separados con una coma) los podemos llevar seguidamente a Maxima para representarlos en un histograma.
| numeros_2dados:[2, 3, 4, 5, 6, 7, 3, 4, 5, 6, 7, 8, 4, 5, 6, 7, 8, 9, 5, 6, 7, 8, 9, 10, 6, 7, 8, 9, 10, 11, 7, 8, 9, 10, 11, 12]$ histogram ( numeros_2dados, nclasses=11, frequency=density, xlabel=”Espacio muestral”, ylabel=”Densidad de probabilidad”, fill_color=orange, fill_density=0.9); |
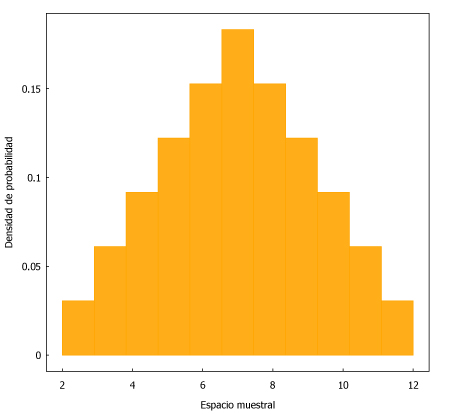
Aquí ya tenemos la posibilidad de realizar preducciones en base a los principios de la estadística. Sabemos que hay unos números más probables (los que están entre el 6 y el 8, siendo el más probable el 7), mientras que lo más improbable es que salgan dos “unos” (suman 2) o dos “seises” (suman 12).
Conclusión
Con estas sencillas simulaciones hemos visto que para tomar decisiones (recordemos que las decisiones se hacen en base a predicciones, y que por ello intercambiamos ambos términos), podemos emplear herramientas matemáticas tanto en el caso completamente determinista (cuando hay leyes), como cuando los fenómenos son aleatorios. La diferencia estriba en que cuando rige el azar, debemos emplear el lenguaje de la probabilidad, entendiendo que cualquier resultado es posible, y que el valor teórico de probabilidad se alcanza en el largo plazo (cuando se repite muchas veces el mismo experimento).
Simplificando mucho, podemos decir que en las ecuaciones deterministas no podemos errar en la predicción si hemos medido bien las variables independientes. Sin embargo, en los fenómenos completamente aleatorios hay una incertidumbre inherente, y nos podemos equivocar aunque apostemos por el resultado más probable.
¿Y todo esto para qué le sirve a un estudiante de Adminitración de Empresas o a cualquier alumno interesado en las Ciencias Sociales? La respuesta (con cierto detalle) la veremos en un posterior post, donde explicaremos que el marketing, y cualquier otra disciplina de las ciencias sociales se mueve a caballo entre el determinismo y el azar, es decir, no vamos a estar en ninguno de los dos extremos que hemos explicado aquí, sino en un estadío intermedio donde se mezclan en las ecuaciones una parte determinista y una parte aleatoria.
