Una variante del método de la secante es el método de la posición falsa (Regula Falsi), que básicamente ejecuta el procedimiento de la secante pero cambiando levemente el algoritmo para que entre dos puntos de dos iteraciones sucesivas siempre se encuentra la solución, de forma análoga a como ocurre con el método de la bisección. Lo haremos, como siempre, desde el punto de vista práctico, y siguiendo a Burden, Faires & Burden (2017).
Función de partida
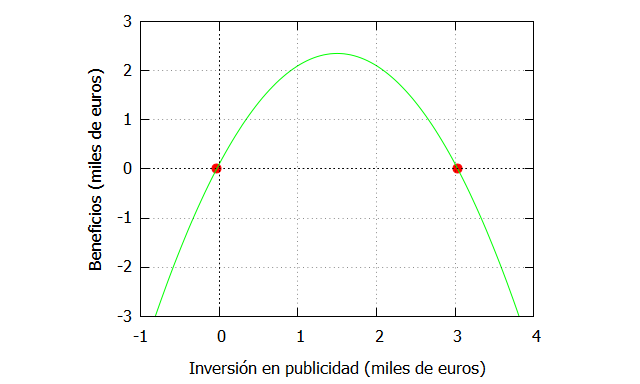
Emplearemos la misma función que en los ejemplos anteriores, donde se relaciona la inversión en publicidad con los beneficios.
| f_ceronegativo:ev(funcion,x=-0.03297097167558977), numer; f_ceropositivo:ev(funcion,x=3.03297097167559), numer; plot2d([[discrete, [[-0.0329709716755897,f_ceronegativo], [3.03297097167559, f_ceropositivo]]], funcion],[x,-1,4],[y,-3,3], [xlabel, “Inversión en publicidad (miles de euros)”], [ylabel, “Beneficios (miles de euros)”], [style, points, lines], [color, red, green], [legend, false]); |
Método de la posición falsa
(1) Objetivo: Aproximarse numéricamente a la solución p de una función , tal que
(2) Condiciones: La función debe ser continua en el intervalo
considerado.
(3) Descripción rápida: Partimos del método de la secante:
Para calcular p2 empleamos la fórmula anterior (tras proveer las semillas p0 y p1). Sin embargo, para calcular p3, usaremos los valores (p2,p1,f(p2),f(p1)) sólo si f(p2) y f(p1) tienen signo opuesto. Si ambos tiene el mismo signo, entonces en lugar del par (p1,f(p1)), escogemos (p0,f(po)). Y se sigue ese mismo criterio para el resto de iteraciones.
(4) Convergencia: Un criterio suficiente (pero no necesario) para que lo haga es que:
Si se cumple la fórmula anterior cuando está en un intervalo alrededor de la raíz entonces la solución converge en cualquier punto de ese intervalo. Para emplear este criterio, hemos de añadir el requerimiento de que la función sea dos veces derivable.
Normalmente, el método de la posición falsa converge de forma más lenta que el de Newton y el de la secante.
(5) Estimación del error: Hay diversas opciones, aunque una de las más recomendables es el error relativo:
Implementación en Maxima
Vamos a implementar el algoritmo partiendo de los dos valores con los que inicíabamos el método de la bisección: [2.5,3.5], que actúan como las primeras semillas en el método de la posición falsa, y vamos a adaptar en Maxima la propuesta de Ramírez (2008):
| falsapos(arg):=block([a:arg[1],b:arg[2],f:arg[3],xm], xm:(a*ev(f,x=b)-b*ev(f,x=a))/(ev(f,x=b)-ev(f,x=a)), if (ev(f,x=xm)*ev(f,x=a)<0) then [a,xm,f] else [xm,b,f] ); ini:[2.5,3.5,-(x^2)+(3*x)+0.1]; for i:1 thru 10 do (print(ini[1]),ini:falsapos(ini)); |
Y nos genera estos resultados:
2.5 2.95 3.021739130434783 3.031481481481481 3.03277399056109 3.03294493097818 3.032967529289182 3.032970516620634 3.032970911521146 3.032970963723678
Para trabajar un poco estos procedimientos, los estudiantes pueden intentar programar una rutina con Maxima donde se codifiquen los procedimientos de Newton, secante y posición falsa, y comparar las aproximaciones.
Conclusión
En este post hemos explicado brevemente en qué consiste el método de la posición falsa. Burden, Faires & Burden (2017) no recomiendan por lo general este método, pero no deja de ser interesante para trabajar las rutinas de programación y para entender los diferentes procedimientos numéricos de búsquedas de raíces.
