Para completar la serie de posts sobre la toma de decisiones en marketing, vamos a ilustrar en qué lugar se encuentran las ciencias sociales frente al determinismo y el puro azar. Y es justo en medio.
De este modo, podemos plantear modelos de predicción que tendrán una parte determinista (mejor llamada “sistemática”) y otra parte aleatoria.
Es importante señalar que, a diferencia de una ecuación determinista como
donde hallábamos F en función del valor de la masa, ahora lo que tenemos es una perspectiva diferente, porque disponemos de valores de la variable independiente, pero también de la dependiente, y lo que queremos hallar es un parámetro (o varios) que desconocemos y que minimizan el error de predicción
Así, tenemos una parte sistemática de la ecuación (lo que conocemos) que es mi, y una parte aleatoria (lo que desconocemos) que es ei. Además, tenemos que plantear dos asunciones básicas: E(ei)=0 y cov(mi, ei)=0. A la ecuación añadidos un término constante α (intercept), que nos indica el valor de la esperanza de la variable dependiente cuando el valor de mi es cero. Si llamamos al β parámetro que queremo estimar (en este caso la aceleración), tenemos la ecuación clásica del modelo de regresión lineal.
Lo que hemos planteado con este modelo es que podemos estimar el valor de la aceleración de la gravedad a través de tener una muestra de i observaciones de la masa y de la Fuerza. Pero sabemos que hay más variables que pueden influir (el lugar de la Tierra, por ejemplo), pero asumimos que esas variables se distribuyen aleatoriamente y no están correlacionadas con las observaciones de la masa (posteriormente hay que testar esas asunciones).
Este modelo se puede estimar por varios métodos estadísticos, pero el más conocido y menos exigente en cuanto a asunciones es el de mínimos cuadrados ordinarios (OLS, en ingés). Ese método consiste en minimizar la suma de los errores (o residuos) al cuadrado, y nos da una estimación de los dos parámetros del modelo: α y β.
Así, el error para cada valor predicho es:
El desarrollo completo de estas ecuaciones se estudia en cursos de econometría y estadística.
Predicción imprefecta
Vamos a comenzar a realizar las simulaciones. Imaginemos que tenemos estos pares de datos de masa y Fuerza observados en diversas mediciones: ([1,9.82],[2,19.9],[3,28.8],[4,36],[5,49])
En wxMaxima se puede realizar un ajuste por mínimos cuadrados empleando el siguiente código sobre ese conjunto de datos:
| modelo:alpha+beta*m$ M:matrix([1,9.82],[2,19.9],[3,28.8],[4,36],[5,49])$ aux:lsquares_estimates(M,[m,F], F=modelo,[alpha,beta])$ f:float(subst(aux, modelo)); |
El output que nos da ese código es 0.366+0.9446*m. Esa es la ecuación de regresión ajustada, es decir, con las estimaciones de α y β.
Lo que podemos hacer ahora es ver qué tal predice el modelo ajustado con respecto a los datos observados, y para ello escribimos el siguiente código:
| g(masa,Fuerza):=block([pred, observado], pred: 9.446*masa+0.366, observado: Fuerza, return(pred-observado)); |
De este modo, podemos valorar cualquier función “g” con los argumentos de la masa y la Fuerza. Una opción es valorar los errores de predicción sobre los puntos observados. Por ejemplo:
g(1,9.82)=0.008
g(2,19.9)=-0.64
g(3,28.8)=-0.096
g(4,36)=2.15
g(5,49)=-1.40
Como puede verse, hay errores en todas las predicciones, unos mayores que otros. Es fácil comprobar que el promedio de esos errores es prácticamente cero.
A continuación, preparamos los datos para representarlos gráficamente, donde vamos a dibujar los datos observados junto con la recta de ajuste
| vectores:transpose(M)$ masas_list:vectores[1]$ Fuerzas_list:vectores[2]$ predicho:9.446*x+0.366$ plot2d([[discrete, |
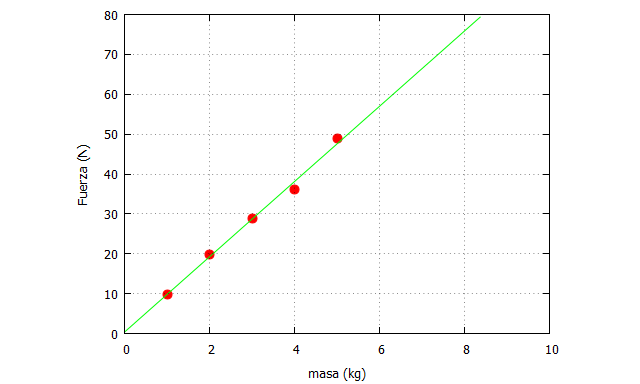
De este modo, podemos realizar predicciones también con valores de la masa fuera del rango observado en el modelo de ajuste, aunque esto hay que hacerlo siempre con mucho cuidado ya que fuera de ese rango puede que la relación funcional cambie.
El ajuste a los datos es excelente, y una medida de ese ajuste se determina en función del cociente de varianzas de los residuos y los datos observados en la variable dependiente. Es lo que se denomina coeficiente de correlación múltiple, varianza explicada, o R-cuadrado:
siendo SCE la suma de cuadrados de los errores, y SCT la suma de cuadrados totales. En este caso, el valor de R-cuadrado=0.992, por lo que es muy bueno.
No obstante, para que el modelo sea considerado válido, debe ser teóricamente plausible y cumplir las asunciones, independientemente de que la varianza explicada sea mayor o menor.
Conclusión
Los estudiantes de marketing pueden comprobar que cualquier decisión basada en modelos estadísticos, combinando una parte sistemática y otra aleatoria, tiene error. La cruda realidad es que en el campo del marketing no vamos a encontrar modelos que se ajusten tan bien a los datos como el mostrado en este ejemplo. Usualmente estaremos bastante alejados de esta situación. En marketing, y en ciencias sociales en general, la incertidumbre es mayor, y también los errores cometidos.
Aquí hemos considerado una única variable independiente, pero los modelos pueden tener varias. Cuanta más información manejemos es probable que los errores disminuyan las decisiones tengan mayor probabilidad de éxito. Pero aun así, nos vamos a equivocar.
Las asignaturas de econometría de la carrera de GADE son esenciales para aprender a realizar análisis de datos. Este post es simplemente un ejemplo introductorio para estimular su entendimiento.
