[MONOTEMA] Seguimos creando material auxiliar para comprender mejor las herramientas de toma de decisiones en marketing. En este post vamos a comentar uno de los aspectos que quizá cuesta un poco más de trabajo entender en las primeras clases de marketing, y es el de emplear el mismo modelo de regresión lineal cuando el modelo teórico es no lineal.
Esta aparente contradicción llama la atención de los estudiantes, y más cuando estamos incidiendo en el hecho de que la no linealidad está presente en la mayoría de los fenómenos que queremos estudiar. Sin embargo, la clave está en entender que la estimación de mínimos cuadrados ordinarios que solemos emplear, también se puede aplicar a modelos no lineales. Y es así, porque la no linealidad está en las variables pero no en los parámetros estimados. Este hecho es fundamental para comprender que con la misma herramienta con la que intentamos hacer predicciones en modelos lineales, también podemos emplearla en modelos no lineales.
Vamos a ilustrarlo con un ejemplo, usando códigos de Stata y MAXIMA, para facilitar que cualquier alumno pueda reproducirlos y hacer probaturas a su antojo.
Generación de la curva no lineal
Elegimos una curva normal de media=5 y desviación típica=1. Por tanto, transformamos la función de densidad normal:
en la siguiente función:
que tiene la característica forma de campana:

Para generar el gráfico anterior, hemos empleado el siguiente código en wxMaxima:
| funcion1:(1/(2*%pi)^0.5)*%e^(-0.5*(x-5)^2)$ plot2d(funcion1, [x,0,10],[style, lines], [color, green], [legend, false], [xlabel,”x”], [ylabel, “y”]); |
Es evidente que se trata de una curva no lineal, pero podemos tratar de realizar predicciones muy ajustadas si planteamos el modelo correcto y lo estimamos por mínimos cuadrados ordinarios (con linealidad en los parámetros).
Ajuste del modelo con Stata
Vamos a emplear ahora uno de los programas más potentes de análisis de datos, y de los más indicados para los profesionales del marketing: Stata.
Para ello, abrimos un archivo en blanco de Stata, y utilizamos el interfaz de comandos que el programa proporciona, llamado “Do-file Editor”, que es simplemente un editor de texto donde se puede escribir un código (secuencia de instrucciones) para ejecutar.
| set obs 1000 generate t = _n drawnorm x, n(1000) means(5) sds(1) gen y=(1/(2*3.1415)^0.5)*exp(-0.5*((x-5)^2)) gen lnx=ln(x) gen lny=ln(y) gen x_cuad=x*x regress lny x x_cuad gen pred=-13.4+(5*x)-(0.5*x_cuad) gen transf_pred=exp(pred) gen dif= y- transf_pred tsset t twoway (tsline dif, lcolor(red) lwidth(vvvthin) xtitle(t) ytitle(Diferencia entre el valor real y el predicho)) |
Explicamos de manera muy sencilla lo que hemos programado. En primer lugar le hemos dicho al programa que genere una muestra de 1000 observaciones, y una variable llamada “t” que es el identificador de cada una de ellas.
Después, le pedimos a Stata que genere para esos 1000 casos una variable Normal llamada “x” con media 5 y desviación típica 1, tal y como hemos mencionado en el apartado anterior.
Ahora debemos asignar una probabilidad a cada uno de esos valores de la variable x, y lo hacemos simplemente espeficiando una variable y que es la función de densidad Normal con media 5 y desviación típica 1.
Para ilustrar que a partir de los valores de x podemos explicar y/o predecir y, tenemos que especificar un modelo que relacione ambas variables. Ese modelo, es obvio que es el regido por la función de densidad Normal, pero ahí no tenemos nada claro cómo encajar nuestro marco de regresión lineal.
Lo que hacemos entonces es tomar logaritmos neperianos a ambos lados de la igualdad:
De este modo:
Si lo reordenamos:
Con esto ya tenemos una disposición muy interesante para realizar la ilustración que pretendíamos.
Si imaginamos ahora que no conocíamos esta especificación exacta de la realidad, pero tenemos el suficiente conocimiento teórico para postular un modelo que trate de describir esos datos, podemos entonces plantear el siguiente modelo de regresión no lineal en las variables, pero lineal en los parámetros:
siendo u el error aleatorio, ruido blanco que desconocemos y que no covaría con x. Entonces planteamos el modelo de regresión con Stata (regress lny x x_cuad), y obtenemos los parámetros estimados correspondientes:

Claro, conseguimos un ajuste prácticamente perfecto, porque hemos hecho un poco de “trampa” a la hora de plantear el modelo (sabíamos el modelo subyacente antes de plantearlo).
Para ilustrar mejor cómo predice el modelo (y que se vean unas mínimas diferencias con las observaciones reales) cogemos sólo el primer decimal de la constante, es decir:
Y entonces generamos el valor predicho por el modelo (gen pred=-13.4+(5*x)-(0.5*x_cuad)). Por último, transformamos el valor predicho con el antilogaritmo neperiano, para compararlo con nuestras observaciones reales. Y generamos el gráfico con Stata.
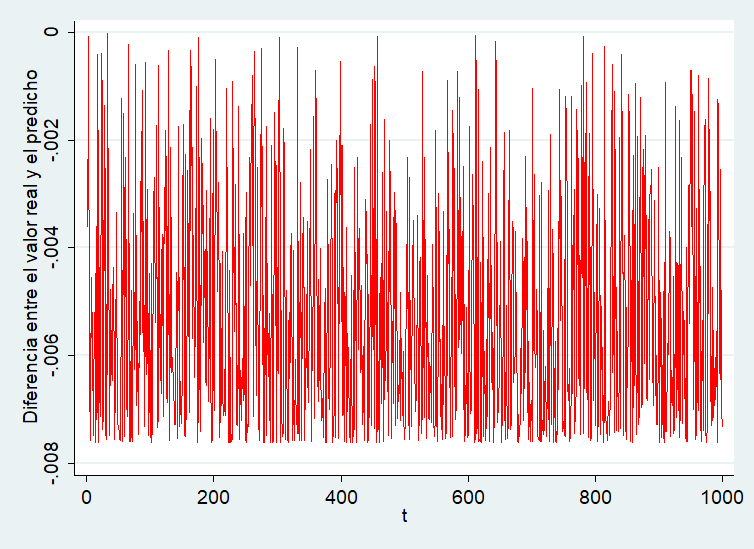
Como puede observarse, los errores son extremadamente pequeños, del orden de milésimas de unidad. Eso quiere decir, que nuestras predicciones son realmente buenas.
Ahora podemos ir a wxMaxima y comparar la curva original de datos observados (funcion1), con la curva de valores predichos (función2)
| funcion1:(1/(2*%pi)^0.5)*%e^(-0.5*(x-5)^2)$ funcion2: %e^(-13.4+5*x-0.5*x^2)$ plot2d([funcion1,funcion2], [x, 0, 10],[style, lines, lines], [color, green, orange], [legend, false], [xlabel,”x”], [ylabel, “y”]); |
Y entonces obtenemos la curva original (en verde) frente a la predicha (en naranja), ambas casi idénticas:
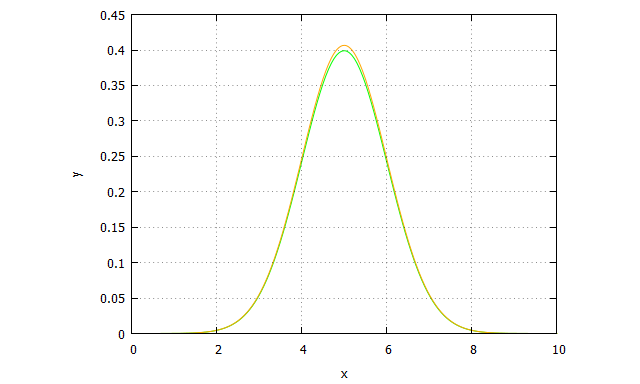
Conclusión
El ajuste por mínimos cuadrados ordinarios es una herramienta muy potente para intentar conocer la realidad que subyace a los datos, independientemente de que la relación entre las variables sea lineal o no lineal.
Sin embargo, y como veremos en posteriores posts, hay que conocer adecuadamente las asunciones que se vinculan a cada modelo propuesto, y testarlas vis a vis con los datos empíricos. Recordemos que las asunciones están dentro de la propia especificación del modelo, por lo que son inherentes a él.
En cualquier caso, y a modo meramente cualitativo, los estudiantes de marketing deben darse cuenta de la importancia que tiene dominar la estadística, para ayudar en la toma de decisiones.
