El Programa Nacional de Toxicología (NTP) de Estados Unidos ha publicado por fin los resultados del estudio que llevaban realizando desde 1999.
Joel M. Moskowitz, investigador de la School of Public Health de la Universidad de California, Berkeley, ha publicado un comentario en su blog sobre un aspecto del informe final que, a su juicio, debería de haber tenido mayor relevancia.
Se trata de los resultados totales de tumores benignos y malignos, los cuales han sido derivados al apéndice. Moskowitz, que lleva muchos años advirtiendo sobre los efectos nocivos de la radiofrecuencia, y en particular de los teléfonos móviles, insiste en que esas proporciones de tumores totales reforzaban aún más las conclusiones del estudio.
Como ya es bien conocido, el estudio del NTP, evaluado también por un panel de expertos externo, ha encontrado evidencia clara de un incremento de riesgo de tumores en el corazón en ratas macho, y también evidencia (aunque menos contundente) de mayor riesgo de cáncer en el cerebro y glándulas suprarrenales. Para ratas hembra y ratones de ambos sexos la evidencia es menos clara.
Estos resultados (en conjunción con la evidencia acumulada en otros estudios) de nuevo reafirman la idea de que la radiación no ionizante puede provocar cáncer, incluso a niveles de exposición cercanos a los límites legales. Por supuesto, hay otros efectos biológicos negativos además del cáncer que también se asocian a estas exposiciones a niveles mucho más bajos.
Sin embargo, es cierto que el estudio deja algunas incógnitas que dificultan su interpretación. El hecho de que los resultados tan concluyentes encontrados en ratas macho no lo sean tanto en los otros 3 grupos, unido a que la esperanza de vida entre ratas macho era mayor (debido a menors problemas crónicos de riñón), añade ruido, ciertamente.
No obstante, mirando a los resultados globalmente, hay poco margen para la duda; existe un efecto negativo de la exposición a radiofrecuencia, que probablemente habría sido más claro si el tamaño de las muestras en los diferentes subgrupos hubiera sido mayor.
El comentario de Moskowitz El profesor Moskowitz indica que la interpretación de los resultados habría sido más clara incluyendo estas tablas en el documento principal (y no en los apéndices).
Como bien indica Moskowitz, este tipo de análisis globales suele tender hacia la hipótesis nula de no efecto, ya que el incremento de tumores en una o unas pocas áreas del cuerpo queda empequeñecido debido a las no incidencia en otras. Es decir, si un agente externo causa claramente un determinado cáncer, realizar un análisis global de todos los tipos de cáncer puede hacer que se concluya que ese agente no está relacionado con el cáncer, cuando obviamente sí lo está pero sólo de un tipo.
No obstante, Moskowitz ve claros indicios en estas tablas de que la incidencia global de tumores es mayor en los grupos expuestos, lo que ayudaría a esclarecer algunas de las incógnitas comentadas anteriormente sobre los resultados.
Complejidad estadística
Lo ideal sería poder acceder a todos los datos de los experimentos para realizar reanálisis estadísticos. Hay que reconocer, sin embargo, que los autores se encontraban ante un diseño metodológico complejo, donde debían tener en cuenta las muertes no asociadas al cáncer, y la falta de independencia entre algunos animales anidados en camadas. Todo esto complica los análisis estadísticos.
Los autores tratan de considerar estos matices en el test Poly-K, con el ajuste de Rao-Scott. En este caso, este es el test estadístico principal de las tablas, y el que muestra si existen diferencias entre las incidencias de cáncer.
Este test indica que para el caso de ratas macho expuestas a GSM, no existen diferencias en tumores malignos con respecto al grupo de control (p=0.100; p=0.081; p=0.197), aunque cuando se tienen en cuenta también las neoplasias benignas, el dibujo se modifica un poco (p=0.061; p=0.009; p=0.096).
Para las ratas expuestas a CDMA el patrón es similar: nos acercamos a la significatividad en los tumores malignos (p=0.509; p=0.031; p=0.076), y también en las neoplasias totales (p=0.009; p=0.014; p=0.210).
Por tanto, parece evidente que los tumores, tanto malignos como benignos se incrementan en los grupos experimentales, expuestos a ambos tipos de señal de radiofrecuencia. Este patrón es innegable; lo que sucede es que los resultados se embarran un poco cuando el máximo efecto sucede para 3W/kg, y no para 6W/kg. Estos resultados pueden ser debidos a la variabilidad muestral, pero como el patrón se repite en todos los casos de esta tabla, dejan algunas dudas sobre la existencia de un posible efecto de hormesis, es decir, sobre la existencia de un fenómeno no lineal de respuesta a la dosis.
Podemos simular los análisis de tendencia en las proporciones, aunque sin tener en cuenta ciertas matizaciones (importantes) de los autores, pero que nos dan una idea de la tendencia lineal del efecto:
Así, podemos realizar varios test de tendencia lineal, y vemos lo siguiente:
| GSM | CDMA | |||
| Ratas totales | Tumores malignos | Todos los tumores | Tumores malignos | Todos los tumores |
| Tendencia lineal | p=0.087 | p=0.008 | p=0.026 | p=0.300 |
| Desviación de la linealidad | p=0.254 | p=0.015 | p=0.136 | p=0.001 |
Esta tabla nos dice que es muy arriesgado apostar por la hipótesis lineal, ya que las desviaciones son significativas para todos los tumores, aunque no llegan a ello en los tumores malignos. De este modo, interpretar el p-valor de la tendencia lineal no tiene sentido en el caso de todos los tumores, y es quizá un pelín arriesgado para los tumores malignos. Aún así, si se apuesta por ello, los resultados están en el entorno de p=0.05 (que recordemos que no es ningún número mágico, sino simplemente un criterio más que ha de ser evaluado con matices considerando la globalidad de los análisis).
Los autores emplean también el test de Fisher para evaluar la incidencia en las camadas, y este análisis es también muy interesante. De nuevo, la inspección de las tablas anteriores nos lleva a concluir que efectivamente existe un efecto significativo en el desarrollo de cáncer, más acusado cuando se tienen en cuenta todos los tumores.
De nuevo podemos realizar un análisis de tendencia:
| GSM | CDMA | |||
| Camadas | Tumores malignos | Todos los tumores | Tumores malignos | Todos los tumores |
| Tendencia lineal | p=0.045 | p=0.011 | p=0.022 | p=0.051 |
| Desviación de la linealidad | p=0.618 | p=0.346 | p=0.273 | p=0.012 |
De nuevo vemos que la hipótesis lineal es cuestionable en algunos casos (todos los tumores en CDMA), pero se sostiene en el resto, mostrando valores significativos.
Para explorar la hipótesis no lineal, podemos implementar polinomios de Lagrange de grado 3. Admitiendo las limitaciones de estas aproximaciones, nos puede dar una idea útil del número de tumores estimado en el rango de densidades de potencia de los experimentos. El siguiente código de Maxima permite obtenerlos y representarlos para el caso de tumores malignos, tanto en la exposición a GSM como a CDMA:
| p1(x):=(x-x1)*(x-x2)*(x-x3)*fx0/((x0-x1)*(x0-x2)*(x0-x3))+ (x-x0)*(x-x2)*(x-x3)*fx1/((x1-x0)*(x1-x2)*(x1-x3))+ (x-x0)*(x-x1)*(x-x3)*fx2/((x2-x0)*(x2-x1)*(x2-x3))+ (x-x0)*(x-x1)*(x-x2)*fx3/((x3-x0)*(x3-x1)*(x3-x2)); x0:0; x1:1.5; x2:3; x3:6; fx0:24; fx1:36; fx2:38; fx3:35; solucion_GSM: expand(p1(x)); p2(x):=(x-x1)*(x-x2)*(x-x3)*fx0_/((x0-x1)*(x0-x2)*(x0-x3))+ (x-x0)*(x-x2)*(x-x3)*fx1_/((x1-x0)*(x1-x2)*(x1-x3))+ (x-x0)*(x-x1)*(x-x3)*fx2_/((x2-x0)*(x2-x1)*(x2-x3))+ (x-x0)*(x-x1)*(x-x2)*fx3_/((x3-x0)*(x3-x1)*(x3-x2)); x0:0; x1:1.5; x2:3; x3:6; fx0_:24; fx1_:26; fx2_:41; fx3_:34; solucion_CDMA: expand(p2(x)); x_:[0,1.5,3,6]; fx_GSM:[24,36,38,35]; fx_CDMA:[24,26,41,34]; sig95: 35; plot2d([[discrete, x_, fx_GSM],[discrete, x_, fx_CDMA],solucion_GSM, solucion_CDMA, sig95], [x,0,6],[y,0,52], [style, points,points, lines,lines, lines, linespoints], [color,red, red, green, orange,black], [xlabel, «Exposición (W/kg)»],[ylabel, «Tumores malignos»], [legend, false]); |
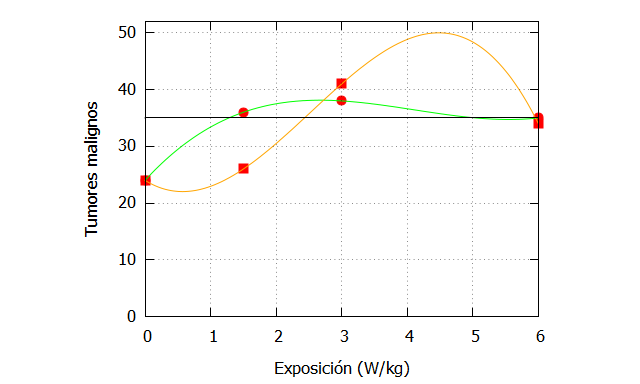
La línea negra marca el límite aproximado de la significación estadística al 95% para un test de Fisher de una cola con respecto al grupo de control (exposición=0). La curva verde es la de GSM, mientras que la naranja es la de CDMA.
Para el caso de tumores totales, podemos programar con Maxima:
| p1(x):=(x-x1)*(x-x2)*(x-x3)*fx0/((x0-x1)*(x0-x2)*(x0-x3))+ (x-x0)*(x-x2)*(x-x3)*fx1/((x1-x0)*(x1-x2)*(x1-x3))+ (x-x0)*(x-x1)*(x-x3)*fx2/((x2-x0)*(x2-x1)*(x2-x3))+ (x-x0)*(x-x1)*(x-x2)*fx3/((x3-x0)*(x3-x1)*(x3-x2)); x0:0; x1:1.5; x2:3; x3:6; fx0:57; fx1:73; fx2:78; fx3:71; solucion_GSM: expand(p1(x)); p2(x):=(x-x1)*(x-x2)*(x-x3)*fx0_/((x0-x1)*(x0-x2)*(x0-x3))+ (x-x0)*(x-x2)*(x-x3)*fx1_/((x1-x0)*(x1-x2)*(x1-x3))+ (x-x0)*(x-x1)*(x-x3)*fx2_/((x2-x0)*(x2-x1)*(x2-x3))+ (x-x0)*(x-x1)*(x-x2)*fx3_/((x3-x0)*(x3-x1)*(x3-x2)); x0:0; x1:1.5; x2:3; x3:6; fx0_:57; fx1_:75; fx2_:76; fx3_:63; solucion_CDMA: expand(p2(x)); x_:[0,1.5,3,6]; fx_GSM:[57,73,78,71]; fx_CDMA:[57,75,76,63]; sig95: 68; plot2d([[discrete, x_, fx_GSM],[discrete, x_, fx_CDMA],solucion_GSM, solucion_CDMA, sig95], [x,0,6],[y,0,85], [style, points,points, lines,lines, lines, linespoints], [color,red, red, green, orange,black], [xlabel, «Exposición (W/kg)»],[ylabel, «Tumores totales»], [legend, false]); |
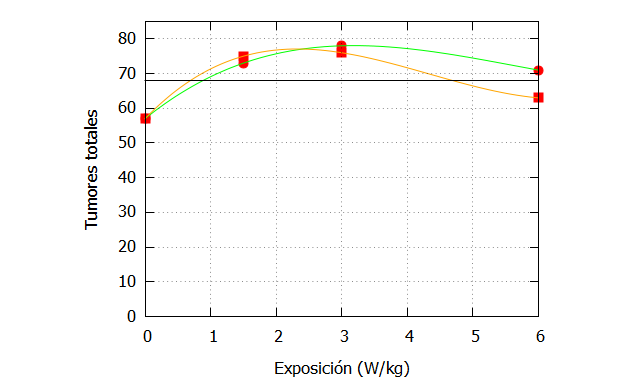
Como antes, la línea negra marca el límite aproximado de la signifiación estadística al 95% para un test de Fisher de una cola con respecto al grupo de control (exposición=0). La curva verde es la de GSM, mientras que la naranja es la de CDMA.
Conclusión
Siempre hemos de ser prudentes en la interpretación estadística, sobre todo con tamaños de muestra pequeños y tamaños de efecto también pequeños. Esto quiere decir que si los efectos no son grandes en magnitud son difíciles de detectar en muestras pequeñas. El concepto de tamaño de efecto pequeño es también matizable, ya que no significa lo mismo cuando estamos hablando de, por ejemplo, renta per cápita, que de vidas humanas.
De nuevo insisto en que, más allá del p-valor, hemos de mirar a los datos en su globalidad. Si hacemos ese ejercicio, y teniendo en cuenta el apoyo de la estadística, la conclusión es poco discutible acerca de la relación causa-efecto entre la radiación de móviles y el desarrollo de tumores.
Otra cosa es la «edulcoración» que parece que algunos miembros del NTP han hecho a posteriori de los resultados argumentando que las densidades de potencia de emisión estaban en el límite o más allá de lo que es legal, y por tanto de la realidad de exposición de los usuarios de teléfonos móviles. Sin embargo, el caso Phonegate y la sobre exposición a radiación no ionizante de múltiples dispositivos inalámbricos cuestionan esa «tranquilizadora» interpretación, que huele más a excusa para que la FDA, la EPA y la FCC no tomen cartas en el asunto. De hecho, la nota de prensa de la FDA del 1 de noviembre no tiene desperdicio.
En cualquier caso, es cierto que la aparante relación no lineal entre la dosis y la respuesta necesita mayor explicación, así como otras incógnitas que el estudio (de 30 millones de dólares) no ha desvelado en su totalidad.
Finalmente, hemos de recordar que este estudio no trata sobre otras enfermedades y trastornos que pudiera ocasionar la exposición a radiofrecuencia y, aunque no deriven en tumores, son de extrema importancia para evaluar este tema en su totalidad.
