BÚSQUEDA DE SOLUCIONES (IV): MÉTODO DE LA SECANTE

[MONOTEMA] Una modificación del método de Newton permite una aproximación a este sin computar la derivada. Se trata del método de la secante, que explicaremos a continuación. Lo haremos, como siempre, desde el punto de vista práctico, y siguiendo a Burden, Faires & Burden (2017).

Función de partida

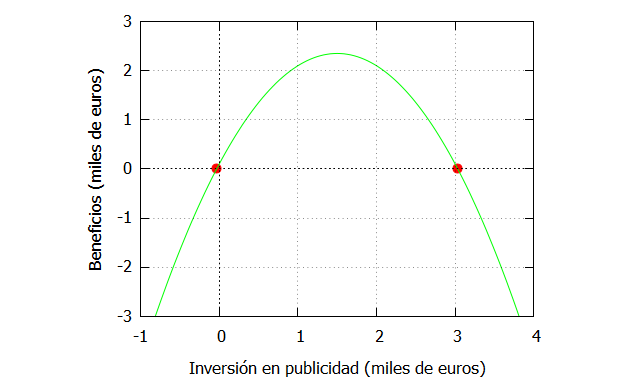
Emplearemos la misma función que en los ejemplos anteriores, donde se relaciona la inversión en publicidad con los beneficios.

f_ceronegativo:ev(funcion,x=-0.03297097167558977), numer; f_ceropositivo:ev(funcion,x=3.03297097167559), numer; plot2d([[discrete, [[-0.0329709716755897,f_ceronegativo], [3.03297097167559, f_ceropositivo]]], funcion],[x,-1,4],[y,-3,3], [xlabel, «Inversión en publicidad (miles de euros)»], [ylabel, «Beneficios (miles de euros)»], [style, points, lines], [color, red, green], [legend, false]);

Método de la secante

(1) Objetivo: Aproximarse numéricamente a la solución p de una función , tal que

(2) Condiciones: La función debe ser continua en el intervalo considerado.

(3) Descripción rápida: Partimos del método de Newton, que recordemos permite construir la sucesión donde:

Pero esa derivada puede ser compleja de calcular, por lo que podemos aproximarla de la siguiente forma:

 De este modo, obtenemos:

(4) Convergencia: Un criterio suficiente (pero no necesario) para que lo haga es que:

Si se cumple la fórmula anterior cuando está en un intervalo alrededor de la raíz entonces la solución converge en cualquier punto de ese intervalo. Para emplear este criterio, hemos de añadir el requerimiento de que la función sea dos veces derivable.

Normalmente, el método de la secante converge de forma más lenta que el de Newton, pero más rápido que otros, como el de la bisección.

(5) Estimación del error: Hay diversas opciones, aunque una de las más recomendables es el error relativo:

Implementación en Maxima

Vamos a implementar el algoritmo partiendo de los dos valores con los que inicíabamos el método de la bisección: [2.5,3.5], que actúan como las primeras semillas en el método de la secante:

f(i):=-x[i]^2+3*x[i]+0.1; x[0]:2.5; x[1]:3.5; for i:2 thru 8 do     (     x[i]:x[i-1]-((x[i-1]-x[i-2])*f(i-1)/(f(i-1)-f(i-2))),     print(i-2,x[i-2])); datos: makelist([[i-2], x[i-2]], i, 2, 8); matriz_resultados:apply(matrix,datos);

Le hemos dicho al programa que nos retorne en el output siguiente:

Como se puede observar, el método converge rápido, y también podemos establecer criterios de parada con programaciones similares a las realizadas con los otros métodos.

Otra forma de hacerlo

El método de la secante, como su propio nombre indica, traza rectas secantes a la función y que pasan por el eje X. La idea es ir aproximando secantes entre puntos de la función hasta converger en la solución. Para ello, es útil considerar la ecuación de la recta que une los puntos (a, f(a)) y (b, f(b)):

Podemos verlo gráficamente si estipulamos que a y b sean 2.5 y 3.5, respectivamente, que son los valores empleados como intervalos en el método de la bisección:

funcion:-(x^2)+(3*x)+0.1; a:2.5; fa:(ev(funcion,x=a)); b:3.5; fb:(ev(funcion,x=b)); secante:((fb-fa)*(x-a)/(b-a))+fa, ratsimp; f_ceronegativo:ev(funcion,x=-0.03297097167558977), numer; f_ceropositivo:ev(funcion,x=3.03297097167559), numer; plot2d([[discrete, [[-0.0329709716755897,f_ceronegativo], [3.03297097167559, f_ceropositivo]]], funcion, secante],[x,-1,4],[y,-3,3], [xlabel, «Inversión en publicidad (miles de euros)»], [ylabel, «Beneficios (miles de euros)»], [style, points, lines, lines], [color, red, green, orange], [legend, false]);

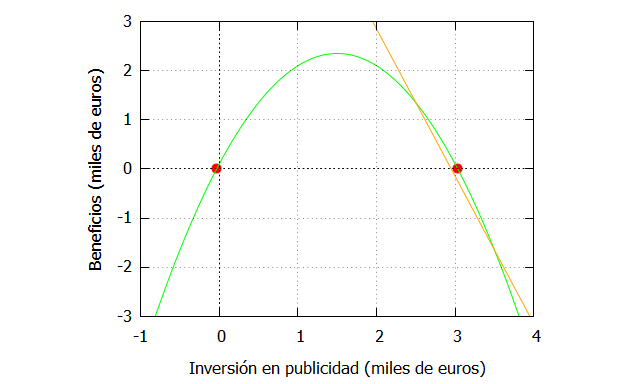
Esta primera recta secante, corta a la función en f(a) y f(b), y ya nos quedamos bastante cerca de la solución. Simplemente hay que seguir trazando secantes iterando entre puntos consecutivos, es decir, el siguiente paso sería realizar el mismo cálculo pero tomando f(b) en lugar de f(a), y f(m) en lugar de f(b), siendo f(m) el valor de la función para el punto m (el punto de corte de la primera secante con el eje X). En Maxima, una forma de computarlo se puede encontrar en Ramírez (2008). Nosotros vamos a adaptar ese código de la siguiente manera: