EXPLORANDO LA NO LINEALIDAD CON MÁXIMA

[MONOTEMA] Hemos explicado que los fenómenos sociales son complejos y que la relación entre las variables a menudo es no lineal, con diferentes formas de curva: rendimientos decrecientes, histéresis, hormesis o efectos acumulativos. También hemos hecho mención a los procesos caóticos.

Para tratar de entender bien esos conceptos en el ámbito de un curso de introducción al marketing voy a proveer de diferentes códigos en Máxima para realizar simulaciones, y explorar gráficamente cómo se pueden comportar esos fenómenos. Máxima es un software gratuito de análisis matemático (descargar aquí).

Decaimiento exponencial

Vamos a representar la siguiente función:

Para ello, escribimos el siguiente código en una sesión con wxMaxima:

f1(x):=block([y1], y1:400*exp(-x), return (y1))$ plot2d(f1,[x,0,40],[y,0,400],[color, blue]);

Básicamente se trata de crear una variable local y1 que contenga la expresión de la función que queremos. El uso de variables locales es siempre adecuado para llevar los cálculos ordenados y evitar problemas en códigos largos. Por tanto, definimos la función f1(x) a través de la variable local y1. Después empleamos la función «plot2d» para llamar a la función que hemos especificado (f1) y decirle el rango en el que queremos que se represente en el eje X y en el eje Y, y también el color (en este caso azul). Es importante señalar que el rango de valores de los ejes es meramente ilustrativo y no tiene ningún significado específico en este y en los siguientes ejemplos.

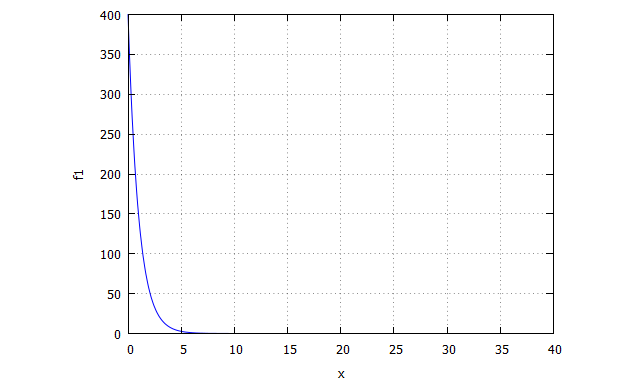
Como puede verse, la función decae muy rápidamente con los primeros valores de x y se va suavizando a medida que x se incrementa. En marketing hay fenómenos que pueden asemejarse a este tipo de curvas, como por ejemplo los relacionados con los de la fluencia (facilidad con la que la información proviene a la mente). Así, la información más fuertemente asociada con el estímulo que estamos valorando llega con mucha más intensidad, pero a medida que seguimos intentando nombrar más asociaciones esa fluencia decae y nos cuesta mucho más trabajo hacerlo.

Esta también es una de las razones por las cuales la comunicación de marketing puede ser importante. Si conseguimos que la marca tenga notoriedad y una alta fluencia, siempre estará en los primeros puestos del conjunto evocado.

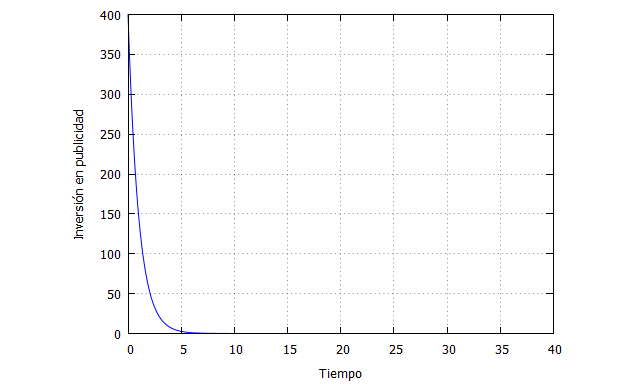
Este tipo de curvas pueden reflejar también el aprendizaje. Por ejemplo pueden representar la caída de la inversión necesaria en publicidad para conseguir los mismos resultados de marketing. Al comienzo del tiempo, una marca necesita una gran inversión para adquirir notoriedad y tratar de persuadir. Sin embargo, con el paso del tiempo, puede seguir manteniendo esos niveles de notoriedad y persuasión con una menor inversión, debido al aprendizaje del consumidor:

Efectos acumulativos

Vamos a representar la siguiente función:

Para ello, escribimos el siguiente código en una sesión con wxMaxima:

f2(x):=block([y2], y2:exp(x), return (y2))$ plot2d(f2,[x,0,40],[y,0,400],[color, magenta]);

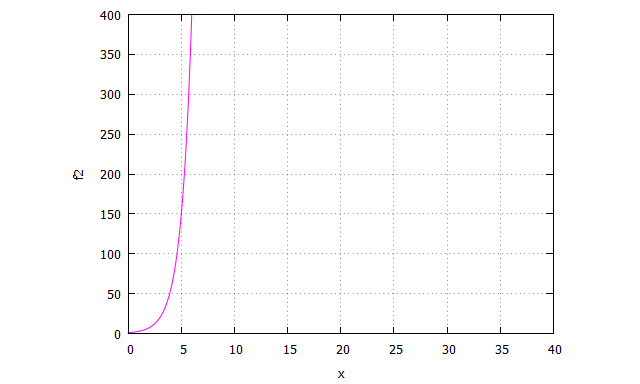
Lo que tenemos aquí es una función que se mueve de manera opuesta al decaimiento, es decir, para los primeros valores de x la función está «dormida», avanza muy poco, pero a partir de un determinado umbral crece rápidamente.

Como comentamos en el post correspondiente, este tipo de relaciones entre variables se da en biología cuando hablamos de tóxicos que se acumulan en nuestro cuerpo, donde hasta un determinado nivel no producen efectos adversos importantes, pero que cuando sobreprasan un punto producen enfermedades u otro tipo de efectos no deseados.

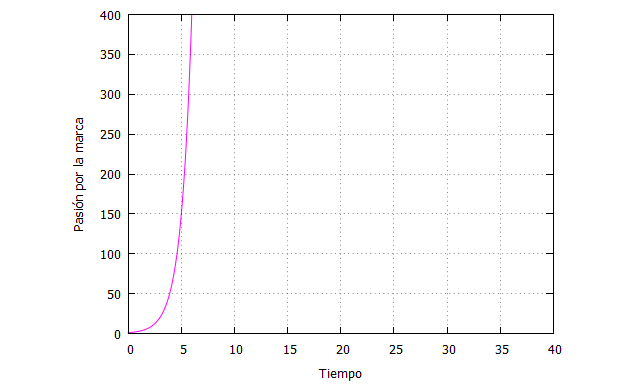
En marketing, estas curvas pueden darse en los procesos de enamoramiento de marcas. Al comienzo, durante las primeras exposiciones la emoción que siente el consumidor crece casi imperceptiblemente, pero después de ir conociendo más cosas sobre la marca, experimentarla, llega un momento en que la pasión se dispara y la persona se vuelve un verdadero fan y defensor de la marca.

Hormesis

Vamos a representar la siguiente función:

Para ello, escribimos el siguiente código en una sesión con wxMaxima:

f3(x):=block([y3], y3:40*x-x^2, return (y3))$ plot2d(f32,[x,0,40],[y,0,400],[color, green]);

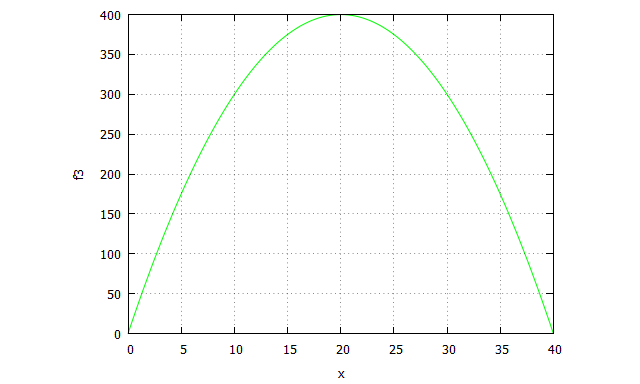
Recordemos que la hormesis es un fenómeno de respuesta a la dosis por la cual existe una dosis adecuada para obtener el máximo efecto, mientras que por encima y por debajo de esa dosis el efecto es más pequeño.

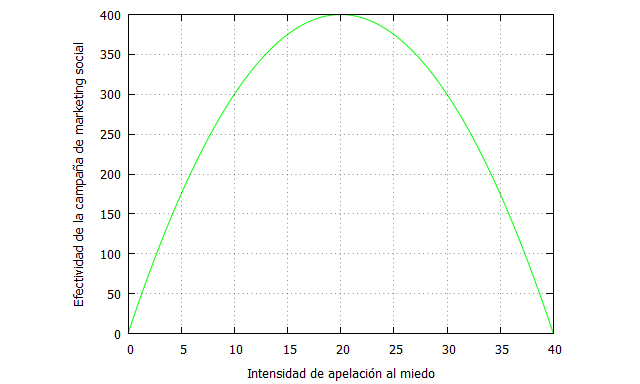
En marketing este tipo de curvas pueden reflejar la relación entre la intensidad de la emisión de publicidad y el efecto sobre la atracción a la marca. Puede que haya un punto donde se maximiza esa atracción, pero si la empresa sigue intensificando sus campañas el consumidor puede empezar a cansarse e incluso comenzar a sentir rechazo por la marca.

Puede también ocurrir en la relación entre la apelación al miedo en publicidad y la capacidad de persuasión de una campaña de marketing social (lucha contra la droga, tabaquismo, accidentes de tráfico, etc.). El miedo funciona, pero a partir de un determinado umbral de intensidad de apelación al terror, la persona puede sentir que es algo irreal, exagerado, o incluso ser tan terrible que trata de distanciarse de ese mensaje que le hace daño. Todo ello disminuye el efecto de la campaña:

Histéresis

Vamos a representar la siguientes funciones:

Para ello, escribimos el siguiente código en una sesión con wxMaxima:

f4_ida(x):=block([y4], y4:96*log(x)-x, return (y4))$ f5_vuelta(x):=block([y5], y5:100+5*log(x)+200*x/(1+x), return (y5))$ plot2d([f4_ida,f5_vuelta],[x,0,40],[y,0,400],[color, red, red],[legend,false]);

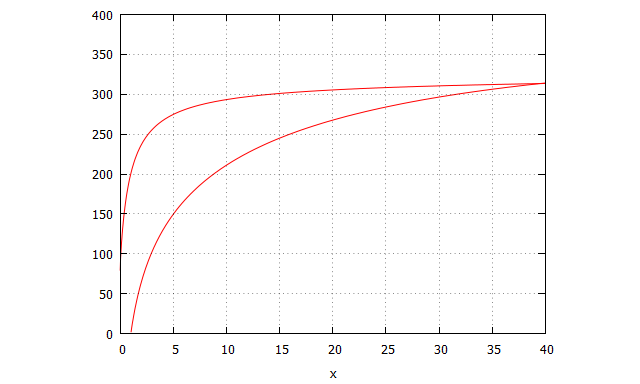
Lo que hemos hecho ahora es crear dos funciones, una para el «camino de ida» y otra para el «camino de vuelta», simulando algo parecido a lo que ocurre en los procesos de histéresis. La primera función comienza creciendo no linealmente hasta que va suavizándose (rendimientos decrecientes), acercándose a un punto de saturación. Refleja, por tanto, una respuesta intensa a los primeros niveles del estímulo. Sin embargo, a medida que la intensidad del estímulo crece la respuesta ya no es tan efectiva, hasta llegar a un punto en el que se necesita una gran variación en el estímulo para conseguir un mínimo de variación en la respuesta.

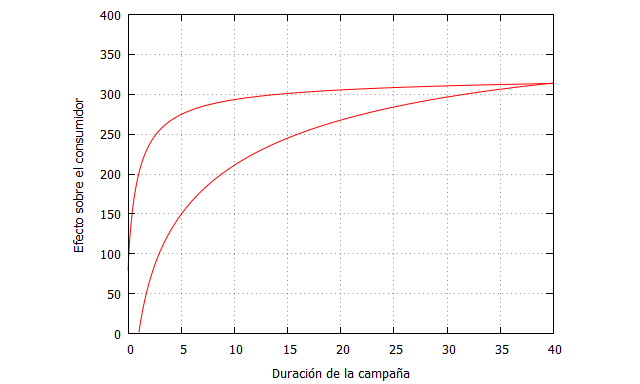
Cuando cesa el estímulo, podemos imaginar que la curva sigue un camino de vuelta que no va por el mismo lugar a medida que el tiempo avanza. Debido a un efecto aprendizaje, aunque el estímulo no exista la respuesta se mantiene o decae hasta un nivel por encima de cero. Esa diferencia entre el origen de las dos curvas (100 en el gráfico) es lo que se llama impregnación, y nos da una idea de cómo permanece el efecto aunque la causa no esté.

En marketing, este tipo de curvas puede reflejar la respueta de los individuos a las campañas publicitarias. Al comienzo, existe una respuesta muy intensa, pero a medida que la campaña se intensifica el consumidor puede cansarse o llegar a un umbral máximo de emoción o persuasión que no crece más aunque sí que lo haga el presupuesto publicitario. Cuando termina la campaña, el consumidor no borra esa respuesta de su mente, la mantiene a un determinado nivel (impregnación), que puede permanecer por un tiempo variable (desde horas hasta años), e influir en futuros comportamientos de compra:

Una visión conjunta

Vamos a representar ahora todas las funciones generadas en el mismo gráfico. Para ello, escribimos el siguiente código en una sesión con wxMaxima:

f1(x):=block([y1], y1:400*exp(-x), return (y1))$ f2(x):=block([y2], y2:exp(x), return (y2))$ f3(x):=block([y3], y3:40*x-x^2, return (y3))$ f4_ida(x):=block([y4], y4:96*log(x)-x, return (y4))$ f5_vuelta(x):=block([y5], y5:100+5*log(x)+200*x/(1+x), return (y5))$ plot2d([f1,f2,f3,f4_ida,f5_vuelta],[x,0,40],[y,0,400],[color, blue,magenta, green,red, red],[legend,false],[xlabel,»Estímulo»], [ylabel, «Respuesta»]);

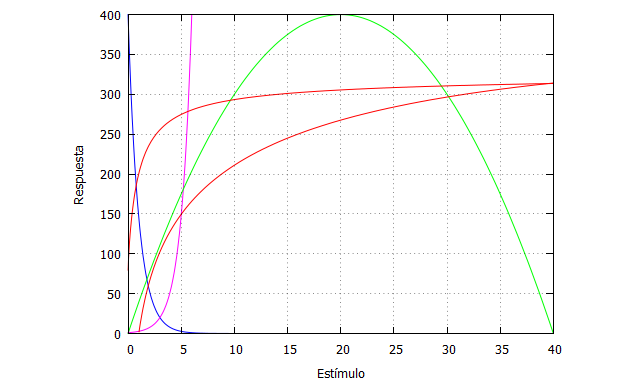
Con este gráfico final observamos la complejidad de las relaciones entre los estímulos de marketing y las respuestas de los consumidores, lo que dificulta mucho la capacidad para hacer predicciones. En marketing, no solemos conocer en detalle las ecuaciones que rigen esas relaciones, sólo podemos tratar de estimarlas con estudios empíricos o realizar aproximaciones teóricas. Es más, en algunas situaciones se podrían dar varios tipos de fenómenos no lineales. Por ejemplo, en la relación entre intensidad de la publicidad y efecto sobre la actitud del consumidor, se pueden dar fenómenos de hormesis, de histéresis, acumulativos, o incluso decaimientos. Depende de muchos factores, y de ahí la extrema complejidad de realizar.

Por tanto, la incertidumbre es alta, pero existen herramientas estadísticas y heurísticas que nos pueden ayudar. Pero recordad (especialmente mis alumnos) que no hay ni varitas mágicas, ni bolas de cristal, ni genios del marketing.