Continuamos analizando las relaciones no lineales entre variables en esta serie de posts para facilitar la comprensión acerca de la complejidad de los fenómenos sociales.
Hoy vamos comentar (sin entrar en detalles profundos) el comportamiento caótico de un sistema. La idea es ver que, incluso en sistemas muy sencillos, con ecuaciones simples, hacer predicciones puede ser una tarea muy complicada.
Vamos a servirnos parcialmente del artículo de Morante & Vallejo (2013), que de manera bastante amigable explican cómo poder simular este tipo de comportamientos en Maxima.
La ecuación lógistica
Emplearemos la ecuación logística (o aplicación logística) para ilustrar ese comportamiento:
donde x es una variable que está entre 0 y 1 y r está entre 0 y 4. En el contexto de los estudios poblacionales, x representa el porcentaje de población sobre el máximo posible, y r una tasa entre la reproducción y la mortandad. Así, si r<1, la mortandad es mayor que la reproducción, y el sistema acabará evolucionando hacia un valor de x=0 en un determinado tiempo t.
Evolución del sistema en función de r
En primer lugar, vamos a realizar varias simulaciones sobre la evolución temporal del sistema en función de varios valores de r: 0.8, 1.8, 2.8, 3.8. Para ello tomamos como valor fijo x=0.9, es decir, el valor de partida es que la población está casi al máximo de lo posible.
Para ello, escribimos el siguiente código en una sesión con wxMaxima:
| F(r,x):=r*x*(1-x)$ /* Ecuación logística*/ load(dynamics)$ /* Carga del paquete para la simulación*/ x_0:0.9$ /* Condición inicial del sistema*/ dominio_x:[y,0,1]$ /* Rango del eje y*/ tiempo:30$ /* Intervalos de tiempo discreto */ r:0.8$ /* Valor asignado a r */ evolution(F(r,x),x_0,tiempo,dominio_x,[color, red],[xlabel, “tiempo”],[ylabel, “x_t_+_1”], [legend, “r=0.8”]); |
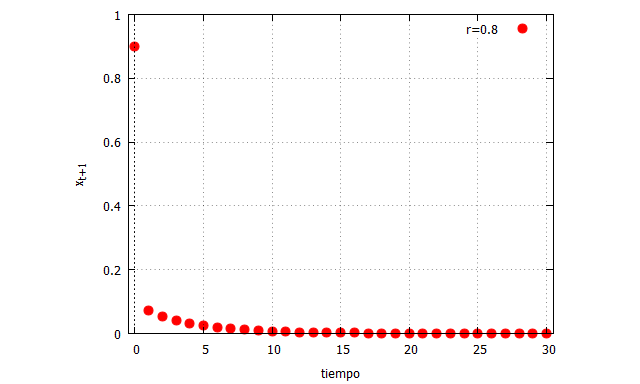
Como era previsible, la población decae hasta que desaparece. Ahora, podemos probar el mismo código de Maxima pero con los valores r=1.8 y r=2.8:
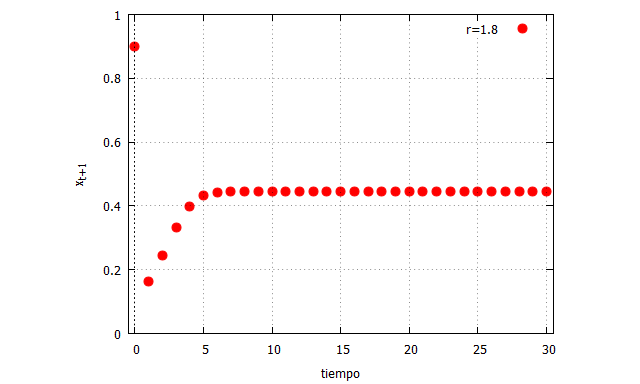
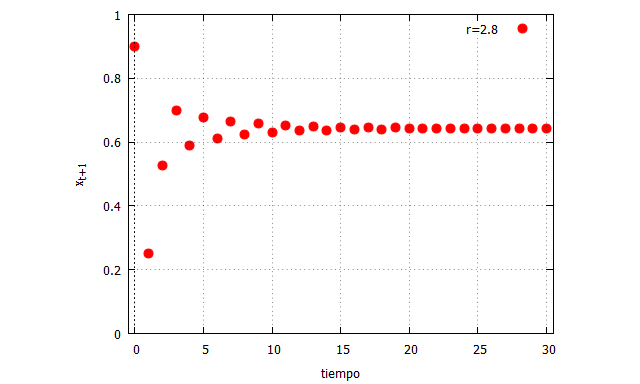
En ambos casos se tiende a un putno de equilibiro en (r-1)/r. Sin embargo, cuando r=2.8, la respuesta del sistema comienza a oscilar entre ese punto, suavizándose progresivamente.
Pero cuando r=3.8, el resultado es el siguiente:
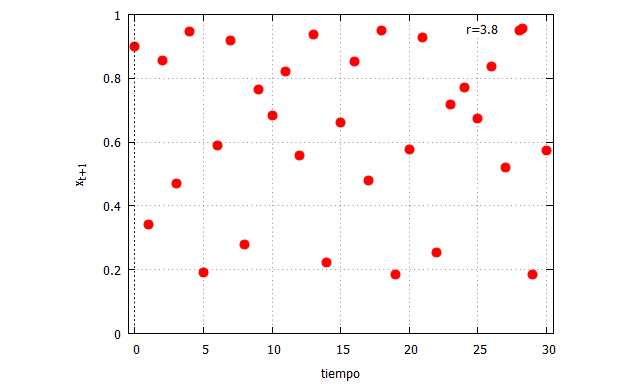
Como puede apreciarse, el sistema se vuelve mucho más oscilante, y no se adivina ninguna tendencia a la estabilidad.
Programación “a mano” de la evolución del sistema
Hemos empleado la función “evolution” de Maxima, que facilita mucho el trabajo. Sin embargo, podemos programar “a mano” el comportamiento del sistema, y así tratar de entenderlo mejor.
Para ello, escribimos el siguiente código en una sesión con wxMaxima:
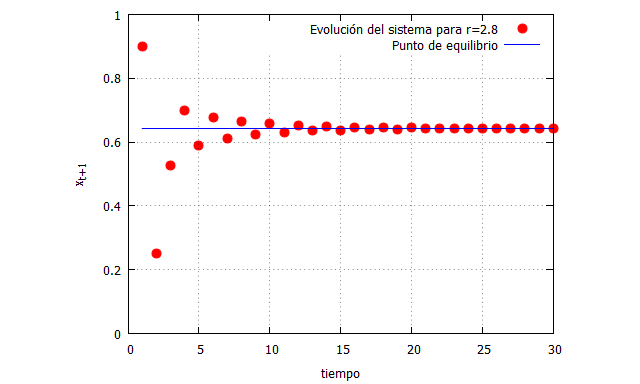
| x[t]:=r*(x[t-1])*(1-(x[t-1]))$ /* ecuación logistica*/ r:2.8$ /* fijamos el valor de r*/ x[1]:0.9$ /* fijamos la condición inicial para t=1*/ datos: makelist([t,x[t]],t,1,30)$ /* hacemos una lista con el resultado de 30 pasos de tiempo*/ matriz:apply(matrix,datos)$ /* convertimos esa lista en una matriz para poder emplearla luego*/ matriz_t: transpose(matriz)$ /* transponemos la matriz anterior para poder usarla en las gráficas*/ t_list: matriz_t[1]$ /* esa matriz traspuesta tiene 2 filas y 30 columnas. La primera fila es la correspondiente a los pasos de tiempo, y es la extraemos aquí */ x_list: matriz_t[2]$ /* extraemos la segunda fila de la matriz, que es la correspondiente al resultado de la función en cada paso de tiempo */ g[t]:=(r-1)/r$ /* creamos una nueva función que representa el punto de equilibrio del sistema, que obviamente depende del valor de r que hayamos fijado. Este valor es una constante, ya que no depende de t */ punto_eq:makelist([t,g[t]],t,1,30)$ /* seguimos el mismo proceso anterior y hacemos la lista de 30 pasos de tiempo */ matriz2:apply(matrix,punto_eq)$ /* convertimos esa lista en una matriz para poder emplearla luego*/ matriz2_t:transpose(matriz2)$ /* transponemos la matriz anterior para poder usarla en las gráficas*/ r_list:matriz2_t[2]$ /* extraemos la segunda fila de la matriz, que es la correspondiente al resultado de la función en cada paso de tiempo */ plot2d([[discrete, t_list,x_list], [discrete,t_list, r_list]], [style,points,lines], [xlabel, “tiempo”],[ylabel, “x_t_+_1”], [x,0,30],[y,0,1],[color,red,blue], [legend, “Evolución del sistema para r=2.8”, “Punto de equilibrio”]); |
Lo que hemos hecho es simplemente reescribir la ecuación logística de esta forma:
Y además hemos añadido la línea que representa el punto de equilibrio. Cualquier lector puede hacer probaturas con otros valores de r y de condición inicial para ver gráficamente cómo evoluciona el sistema.
 Dependencia sensible
Dependencia sensible
Una de las características de los procesos caóticos (probablemente la más conocida, y quizá la más inquietante) es la extrema dependencia de las condiciones iniciales. Así, cambios ínfimos en el valor de la variable que inicia el ciclo de evolución hace evolucionar al sistema de forma totalmente diferente.
Para realizar una prueba visual, hemos tomado dos valores de inicio: 0.900 y 0.899, es decir, una milésima de diferencia entre ambos valores.
Para ello, escribimos el siguiente código en una sesión con wxMaxima:
| x[t]:=r*(x[t-1])*(1-(x[t-1]))$ r:3.8$ x[1]:0.900$ datos: makelist([t,x[t]],t,1,30)$ matriz:apply(matrix,datos)$ matriz_t: transpose(matriz)$ t_list: matriz_t[1]$ x_list: matriz_t[2]$ g[t]:=r*(g[t-1])*(1-(g[t-1]))$ g[1]:0.899$ datos2:makelist([t,g[t]],t,1,30)$ matriz2:apply(matrix,datos2)$ matriz2_t:transpose(matriz2)$ g_list:matriz2_t[2]$ plot2d([[discrete, t_list,x_list], [discrete,t_list, g_list]], [style,lines,lines], [xlabel, “tiempo”],[ylabel, “x_t_+_1”], [x,0,30],[y,0,1],[color,red,blue], [legend, “Condición inicial=0.900”, “Condición inicial=0.899”]); |
El código simplemente refleja la programación de dos funcions “x[t]” y “g[t]”, ambas idénticas, con la única diferencia de esa milésima en las condiciones iniciales. Los resultados para 30 pasos temporales se muestran en el siguiente gráfico:
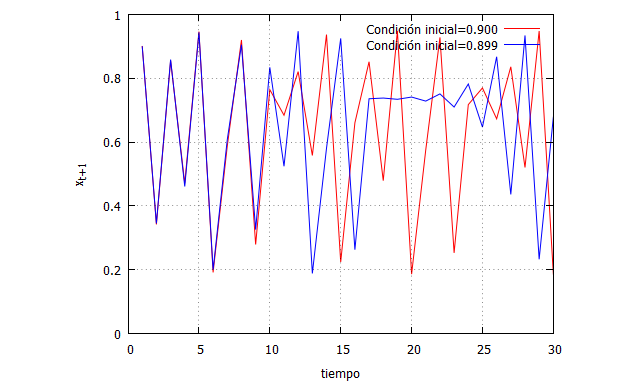
Como se puede apreciar, ambos sistemas comienzan de manera muy parecida su evolución, pero a partir de 10 pasos temporales empiezan a diverger hasta que el comportamiento de uno hace imposible la predicción del comportamiento del otro.
Conclusión
Los sistemas caóticos pueden tener ecuaciones muy simples, pero pese a esa simplicidad los hacen puntualmente impredecibles, aunque para determinados sistemas las órbitas pueden encontrarse en un espacio delimitado, llamado atractor.
Para las ciencias sociales, y especialmente para el marketing, lo mostrado en este post debe hacer reflexionar a los estudiantes sobre qué es la impredecibilidad y cómo entenderla y afrontarla.
