En el contexto de gran incertidumbre en las ciencias sociales, los estudiantes de Administración de Empresas se introducen (sólo un poco) en diferentes técnicas de predicción. Sin embargo, es clave entender que, aunque se consigan buenas aproximaciones a las ecuaciones que rigen un modelo de predicción, el resultado final de ésta puede distar de la realidad de manera importante.
En este post, vamos a hacer unas simples simulaciones, con el fin de ir incorporando los conocimientos que se van adquiriendo en la carrera, para evaluar en qué medida una buena aproximación puede ser útil o no.
Las ventas de un producto
Imaginemos que las ventas de un producto a lo largo del próximo año van a ser las siguientes:
| Enero | 0 |
| Febrero | 2 |
| Marzo | 6 |
| Abril | 12 |
| Mayo | 20 |
| Junio | 30 |
| Julio | 42 |
| Agosto | 56 |
| Septiembre | 72 |
| Octubre | 90 |
| Noviembre | 110 |
| Diciembre | 132 |
| Total año | 572 |
Podemos representar esas ventas con el siguiente código en una sesión de wxMaxima:
| draw2d(fill_color=orange, yrange=[0,150], fill_density=1, xlabel=»Meses», ylabel=»Unidades vendidas», bars([1,0,1],[2,2,1],[3,6,1],[4,12,1],[5,20,1],[6,30,1], [7,42,1],[8,56,1],[9,72,1],[10,90,1], [11,110,1],[12,132,1])); |
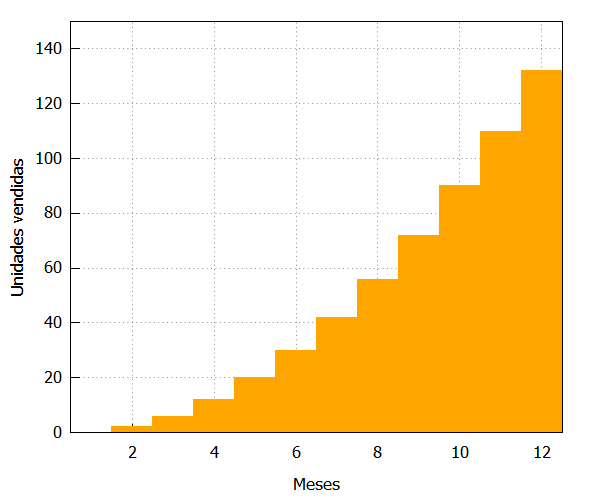
Esas ventas, en realidad, no las sabemos, pero hemos tenido la destreza y el acierto de plantear un modelo matemático que las predice muy bien. Para ello, disponemos de la siguiente función:
donde y son las ventas y x el número de mes (desde 1 hasta 12).
Incorporamos la curva al gráfico anterior:
| funcion:x^2-x; draw2d(fill_color=grey, yrange=[0,150], fill_density=0, xlabel=»Meses», ylabel=»Unidades vendidas», bars([1,0,1],[2,2,1],[3,6,1],[4,12,1],[5,20,1],[6,30,1], [7,42,1],[8,56,1],[9,72,1],[10,90,1], [11,110,1],[12,132,1]), color=orange,line_width=4,explicit(funcion,x,0,12)); |
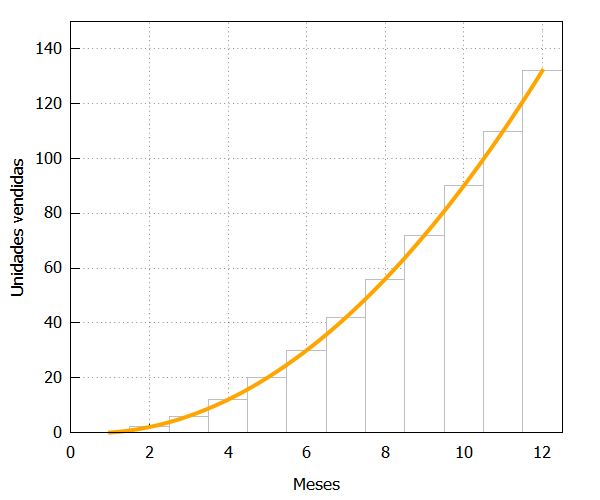Y vemos como el área entre los puntos donde está definida la función (0 y 12), es una buena aproximación a las ventas totales:
| draw2d(fill_color=grey, yrange=[0,150], fill_density=0, xlabel=»Meses», ylabel=»Unidades vendidas», bars([1,0,1],[2,2,1],[3,6,1],[4,12,1],[5,20,1],[6,30,1], [7,42,1],[8,56,1],[9,72,1],[10,90,1], [11,110,1],[12,132,1]), color=orange,fill_color=orange, filled_func=true,line_width=4, explicit(funcion,x,0,12)); |
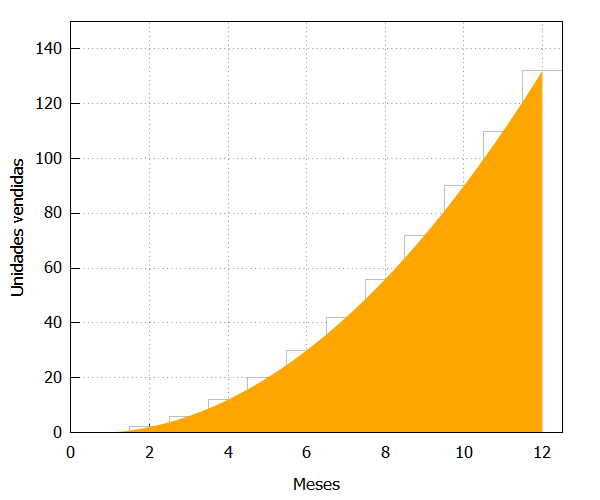El cálculo del área bajo la curva puede hacerse fácilmente en Maxima con este código:
| funcion:x^2-x;integrate(funcion,x,0,12); |
Y el valor es de 504. De este modo, hemos conseguido una estimación de las 572 ventas reales, con un error relativo del 11.9%.
Es sencillo ver que el área de cada barra (base x altura) representa las unidades vendidas (la base siempre es 1), y la suma del área de todas las barras es 572 unidades. Nuestra función hace un buen trabajo, pero está definida de manera continua en el intervalo (0,12), y no de manera discreta. He ahí la diferencia, y por eso la integral reporta una aproximación, que sería cada vez mejor en la medida en que el número de puntos discretos se incrementara (los rectángulos fueran cada vez más finos).
Es decir, aunque tenemos una muy buena función que describe los datos empíricos, cometemos errores de predicción. Esa función continua es una aproximación que hemos considerado necesaria, porque en algún momento podríamos tener la intención de predecir las ventas de manera quincenal, por ejemplo, a 15 de octubre. De este modo, el mes sería 10.5, y necesitamos una función continua definida en (0,12) para poder realizar la predicción.
Si queremos predecir lo que se venderá en un mes determinado, podemos emplear la integral definida entre el mes en cuestión y el mes anterior. Por ejemplo, si queremos saber lo que venderemos el mes 6, integraremos entre 5 y 6, y se queremos saber lo que venderemos hasta el mes 6, entonces integraremos entre 0 y 6.
| funcion:x^2-x;integrate(funcion,x,5,6);integrate(funcion,x,0,6); |
Así, para el mes de junio la previsión será (redondeando) de 25 unidades vendidas (30 serían las reales), mientras que en el primer semestre la predicción sería de 54, cuando la realidad sería 70.
Una buena aproximación (de la aproximación) empeora la predicción
Pese a que tenemos una función que se ajusta muy bien a la realidad, las predicciones no son exactas, y como hemos visto tienen errores. ¿Pero qué sucede si no hemos sido tan afortunados de encontrar una función tan buena como la anterior, y sólo es una buena aproximación a ella?.
Podemos simular de nuevo lo que pasaría, empleando el desarrollo de Taylor de la función descrita, en este caso, sólo hasta el primer término. Para ello, elegimos como entorno el punto medio del rango de datos, es decir, el mes 6 (junio). Usaremos el siguiente código:
| funcion:x^2-x;funcion_aproximada:taylor(funcion,x,6,1);plot2d([funcion,funcion_aproximada],[x,0,12],[y,0,150]); |
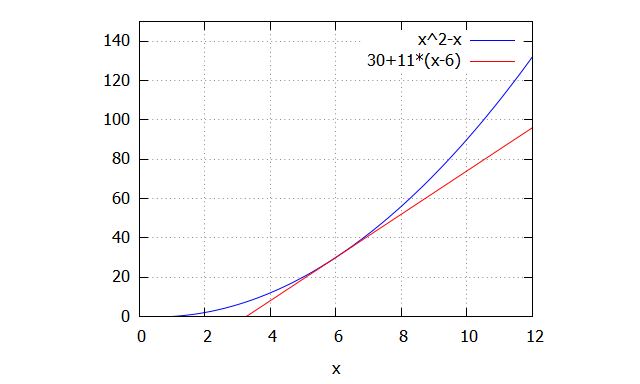Como se aprecia en el gráfico anterior, hemos realizado una aproximación lineal a la función cuadrática original. Visualmente se puede asegurar que la predicción será peor, y que habrá una infra estimación severa con esta nueva función lineal:
| funcion_aproximada:taylor(funcion,x,6,1);integrate(funcion_aproximada,x,0,12); |
El resultado predicho para el total anual es de 360, muy lejos delos 572 reales, también muy lejos de los 504 de la función no lineal. De este modo, el error relativo sería del 37.1%, ciertamente inasumible.
Conclusión
Tomar decisiones en marketing es siempre complejo, debido a la alta incertidumbre asociada con los fenómenos sociales. Las herramientas matemáticas pueden ayudar a encontrar funciones que nos permitan acercarnos a una predicción aceptable.
Pero, como acabamos de ver, incluso aproximaciones excelentes nos proporcionan errores de cierta entidad. Si, además, no conseguimos llegar a encontrar el modelo adecuado y empleamos aproximaciones lineales puede que los errores sean inaceptables.
Obviamente, lo descrito aquí es sólo una forma de ilustrar este problema. Hay múltiples opciones para intentar encontrar buenos modelos. Sin embargo, la idea subyacente sigue siendo la misma; la complejidad lo «complica» todo.