CAMPOS DIRECCIONALES, COMENZANDO A REPRESENTAR LA COMPLEJIDAD

Avanzando un poco más en la introducción a la complejidad de los fenómenos sociales, los alumnos de marketing de GADE se pueden encontrar con la dificultad de enteder la representación de la dinámica de los sistemas acoplados, como el de Lotka-Volterra.

Por ello, en este post vamos a comenzar con los primeros pasos para su comprensión, tratando de trabajar el concepto de campos direccionales y la representación de trayectorias sencillas.

Ecuación diferencial de partida

Comenzamos con uno de los ejemplos más simples que podemos plantear:

Vemos que esta ecuación tiene dos variables, una independiente (t) y otra dependiente (y). La primera de ellas es el tiempo, y la segunda es, por ejemplo, la población de individuos. De este modo, el cambio de la población de individuos con respecto al tiempo depende únicamente de los individuos que hay en cada momento.

Pese a que es una ecuación muy simple, refleja un fenónemo no lineal, que podemos programar así en Maxima:

ecuacion1: ‘diff(y,t) -y=0; solucion1: ode2(ecuacion1,y,t);

Lo que hemos hecho en este código es reformular la ecuación como «ecuacion1»:

Y luego usar función «ode2» de Maxima para resolver la ecuación diferencial ordinaria, en este caso de primer orden, a la que hemos llamado «solucion1».

Maxima nos dice que la solución es:

donde C representa una constante de integración. Cualquier alumno puede intentar llegar a esta misma solución integrando a mano:

que generarán dos constantes de integración que se pueden aglutinar en C.

Llamaremos D=B-A y tomamos exponenciales:

Por tanto, podemos espeficiar sin problema que que , ya que es un número constante, y llegamos a la solución anterior:

Para hallar el valor de C tenemos que especificar unas condiciones iniciales, es decir, cuánto vale y cuando t es cero (que es normalmente la condición de partida). En este caso especificamos que hay 1 individuo cuando el tiempo es 0 (y=1 , t=0):

solucion: ic1(solucion1,y=1,t=0);

La solución final es:

Por tanto, C=1, y ya podemos representar gráficamente la solución

plot2d(%e^t, [t,0,3],[y,0,10], [xlabel, «t»], [ylabel, «y»]);

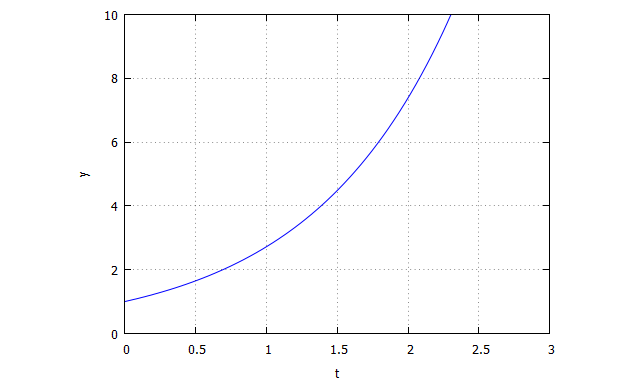
Vemos como la población va creciendo exponencialmente en el tiempo.

Campos direccionales

Los campos direccionales son una forma de representar el camino que van a seguir las trayectorias de cada solución posible de la ecuación diferencial. Para cada punto (i,j) del plano (t,y), es decir, del plano (tiempo, individuos), tenemos una pendiente de la recta, ya que sabemos que una derivada representa precisamente eso:

Por tanto, tenenmos tantas derivadas (j,i) como puntos consideremos. Y una pequeña recta (o flecha) representando el valor de la derivada en esos puntos es lo que se llama campo direccional. Como esas rectas son tangentes a las soluciones, tenemos una especie de camino que esas soluciones deben seguir. Y lo tenemos aunque todavía no hayamos calculado esas soluciones.

Lo podemos obtener con Maxima escribiendo el siguiente código:

load(drawdf)$ drawdf(y,[t,y],[t,0,5], [y,0,5],[xlabel=»t»], [ylabel=»y»]);

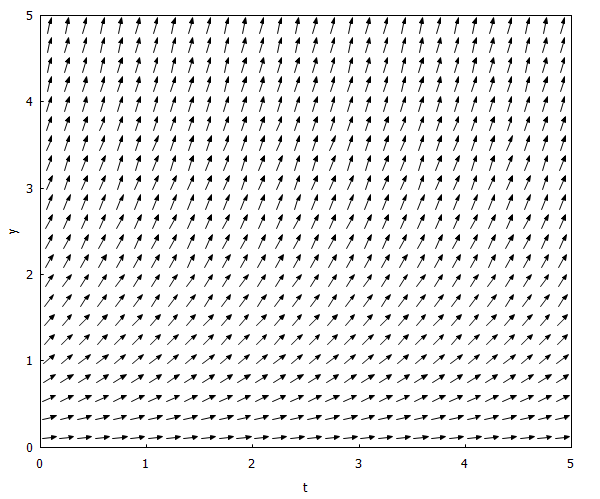
Y ahora simplemente le añadimos al código anterior la trayectoria en el punto (y=1 , t=0):

load(drawdf)$ drawdf(y,[t,y],[t,0,3], [y,0,10],[xlabel=»t»], [ylabel=»y»],[trajectory_at,0,1]);

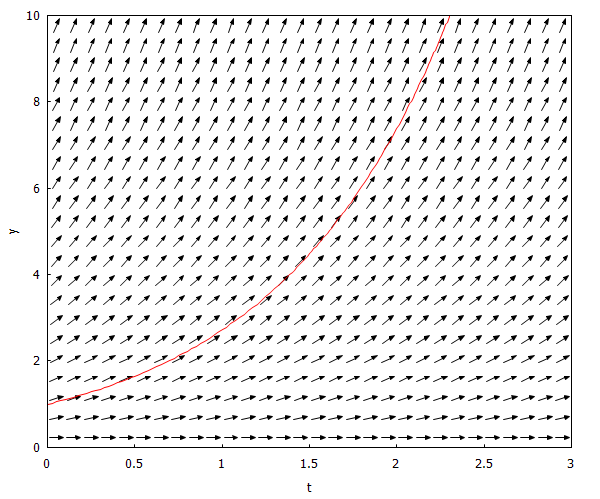
Y, como puede apreciarse, en rojo tenemos la misma curva exponencial que representábamos al comienzo tras resolver la ecucación diferencial para esas condiciones iniciales.

Manualmente podríamos hacerlo simplemente calculando la derivada en cada punto y luego computando el arcotangente para saber el ángulo de inclinación de la recta.

Si las condiciones iniciales cambian, la solución de la ecuación también, y evocionará en el tiempo siguiendo el camino que nos marcan los campos direccionales. Por ejemplo, podemos añadir varias trayectorias más representando condiciones inciales diferentes.

load(drawdf)$ drawdf(y,[t,y],[t,0,3], [y,0,10],[xlabel=»t»], [ylabel=»y»],[trajectory_at,0,0],[trajectory_at,0,1],[trajectory_at,0,2],[trajectory_at,0,3],[trajectory_at,0,4]);

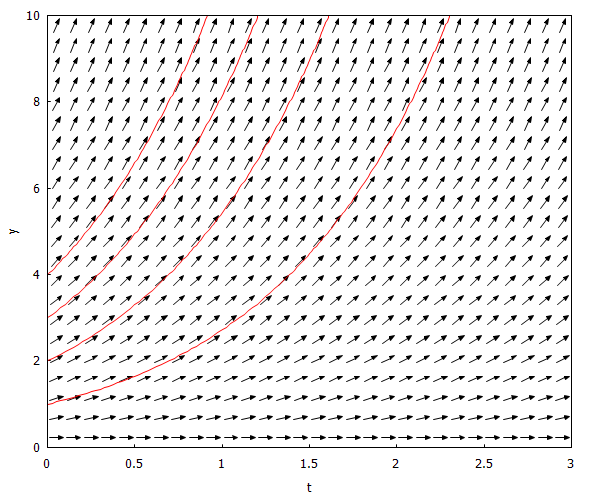
Observese que, aunque le hemos pedido una trayectoria en (0,0), no la ha dibujado. Y no lo ha hecho porque no es posible ninguna trayectoria, ya que en el tiempo cero le hemos dicho que no hay individuos. Como el cambio de individuos con el tiempo (la derivada) depende del número de individuos únicamente en cada estado de tiempo, si hay cero individuos al comienzo no es posible ninguna evolución, y siempre será cero.

Conclusión

En este primer acercamiento a la representación de la complejidad con ecuaciones diferenciales, hemos aprendido a definir los campos direccionales a partir de la especificación de la ecuación diferencial.

Entender este simple ejemplo nos ayudará a avanzar en el análisis de sistemas dinámicos interdependientes, objetivo al que nos iremos acercando poco a poco en sucesivos posts.