BÚSQUEDA DE SOLUCIONES (II): METODO DEL PUNTO FIJO

Continuamos buscando los ceros de una función con aproximaciones numéricas. Tras ver el método de la bisección vamos a continuar con el método del punto fijo. Lo haremos, como siempre, desde el punto de vista práctico, y siguiendo a Burden, Faires & Burden (2017).

Función de partida

Emplearemos la misma función que en el método de la bisección, donde se relaciona la inversión en publicidad con los beneficios.

Lo primero que vamos a hacer es representar esa función en Maxima, tal y como hicimos en el post anterior:

funcion: -x^2+3*x+0.1; plot2d(funcion,[x,0,4],[y,-3,3], [xlabel, «Inversión en publicidad (miles de euros)»], [ylabel, «Beneficios (miles de euros)»], [color, green]);

Pero ahora vamos a expandir el eje de las X, porque nos interesa por motivos ilustrativos representar el corte en el tramo negativo:

funcion: -x^2+3*x+0.1; plot2d(funcion,[x,-1,4],[y,-3,3], [xlabel, «Inversión en publicidad (miles de euros)»], [ylabel, «Beneficios (miles de euros)»],     [color, green]);

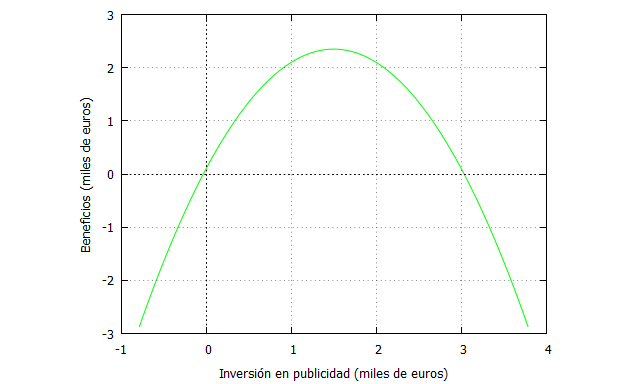
Y vemos que tenemos dos ceros (las dos veces que corta al eje X). Dijimos que la parte negativa no estaba dentro del dominio de la función, pero nos interesa representarla para ver lo que ocurre con la iteración del método del punto fijo.

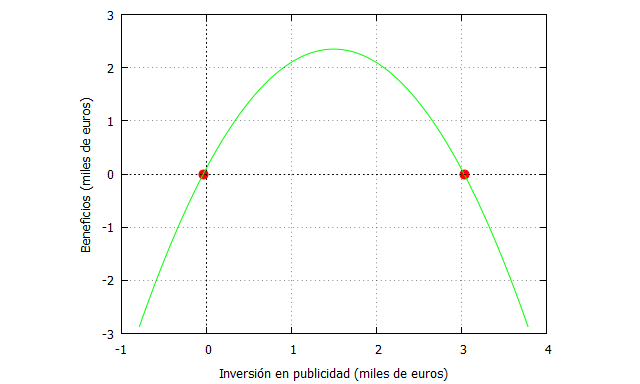
De este modo tenemos dos ceros de la función  y .

Podemos representar esos puntos en el gráfico anterior de la siguiente manera:

f_ceronegativo:ev(funcion,x=-0.03297097167558977), numer; f_ceropositivo:ev(funcion,x=3.03297097167559), numer; plot2d([[discrete, [[-0.0329709716755897,f_ceronegativo],                 [3.03297097167559, f_ceropositivo]]], funcion],[x,-1,4],[y,-3,3],      [xlabel, «Inversión en publicidad (miles de euros)»],      [ylabel, «Beneficios (miles de euros)»], [style, points, lines], [color, red, green], [legend, false]);

 

Método del punto fijo

(1) Objetivo: Aproximarse numéricamente a la solución p de una función , tal que

(2) Condiciones: La función debe ser continua en el intervalo considerado.

(3) Descripción rápida: Si la función , entonces podemos construir la función . De este modo, hemos de escribir nuestra función original como . Esto significa para que haya un cero , es decir, que haya una x despejada en uno de los lados de la igualdad.

(4) Convergencia: No siempre converge. Un criterio suficiente (pero no necesario) para que lo haga es que  , donde es una constante positiva. Si el método converge cuadráticamente.

(5) Estimación del error: Hay diversas opciones, aunque una de las más recomendables es el error realtivo:

Implementación en Maxima

El primer paso, por tanto es crear la expresión a partir de la función original. Suele haber varias formas de hacerlo, en este caso:

Por tanto, tenemos que:

Dibujemos con Maxima todas las funciones:

f(x):= -x^2+3*x+0.1; g1(x):=((x^2)/3)-(0.1/3); g2(x):=(-0.1/(-x+3)); plot2d([f(x),g1(x),g2(x), x],[x,-1,4],[y,-3,5] , [xlabel, «Inversión en publicidad (miles de euros)»],      [ylabel, «Beneficios (miles de euros)»], [style, lines, lines, lines], [color, green, red, blue, black],      [legend, «f(x)», «g1(x)», «g2(x)», «y=x»]);

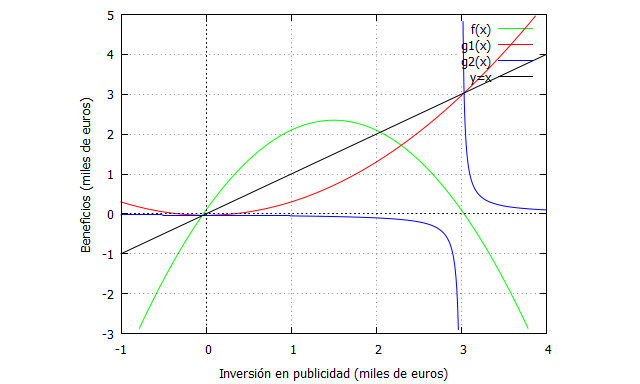
Como se puede apreciar, la recta corta a  y en el valor de x que corresponde a las soluciones de . No vamos a escoger porque tenemos una singularidad en x=3, y por tanto la función no es continua en un entorno cercano a la solución positiva.

Vamos a programar con Maxima el algoritmo, que es bastante sencillo. Para ello, empleamos un bucle con 15 iteraciones, comenzando en 3 como semilla inicial.

g1(i):=(((x[i])^2)/3)-(0.1/3); x[0]:3; for i:1 thru 15 do( x[i]:g1(i-1),print(i,»_Iteración», x[i-1],g1(i-1))); datos: makelist([i,»Iteración»,x[i-1],g1(i-1)], i, 1,15); matriz_resultados:apply(matrix,datos);

Le hemos dicho al programa que nos retorne en el output siguiente:

Como puede observarse, cada imagen de x es el valor de prueba de la siguiente iteración, hasta aproximarnos a la solución. Pero, atención, la solución es negativa, la que no nos interesaba por no tener sentido en nuestro ejemplo.

¿Por qué no converge a la solución positiva pese a que hemos escogido una semilla muy cercana a la solución real?

Si cogemos un intervalo en las proximidades de la solución y lo comparamos con , veremos que no se cumple esa condición. Por ejemplo, en el intervalo [2.5, 3.5] que es el que usamos en el método de la bisección, podemos coger x=3 y comprobar lo que sucede:

En cualquier otro punto de ese intervalo no se cumple el criterio suficiente para la convergencia. No obstante, podría haber convergencia (ya que el criterio no es necesario), pero hemos comprobado que no es así.

El método del punto fijo se va hacia la solución en el eje negativo de las X, donde sí que en un intervalo cercano se cumple esa condición. Por ejemplo, en el intervalo [-1,0].

Aceleración de Aitken

La convergencia se puede acerlerar imlpementando el método de Aitken, donde se construye una nueva sucesión a partir de los 2 primeros términos de la original (la calculada por el método numérico, en este caso del punto fijo):

Podemos programar en Maxima el método de Aitken en conjunción con el de punto fijo, de la siguiente forma:

g1(i):=(((p[i])^2)/3)-(0.1/3); p[0]:3; for i:1 thru 15 do( p[i]:g1(i-1), p_aitken[i+2]:p[i-1]-(((p[i]-p[i-1])^2)/(p[i+1]-2*p[i]+p[i-1]))); datos: makelist([i,»Iteración»,p[i-1],g1(i-1), p_aitken[i+2]], i, 1,15); matriz_resultados:apply(matrix,datos);

Al implementar ese código en Maxima, se puede ver que la convergencia es más rápida.

Conclusión

En este post hemos dado unas pinceladas sobre la implementación del método de punto fijo, encontrando que pueden existir problemas de convergencia para determinadas funciones. Asimismo, la aceleración de Aitken puede emplearse para intentar aproximarse a la solución con menor coste computacional.