BÚSQUEDA DE SOLUCIONES (III): METODO DE NEWTON

Seguimos en la búsqueda de los ceros de una función con aproximaciones numéricas. Tras ver el método de la bisección y el método del punto fijo,  vamos a continuar con el método de Newton, también conocido como Newton-Raphson. Lo haremos, como siempre, desde el punto de vista práctico, y siguiendo a Burden, Faires & Burden (2017).

Función de partida

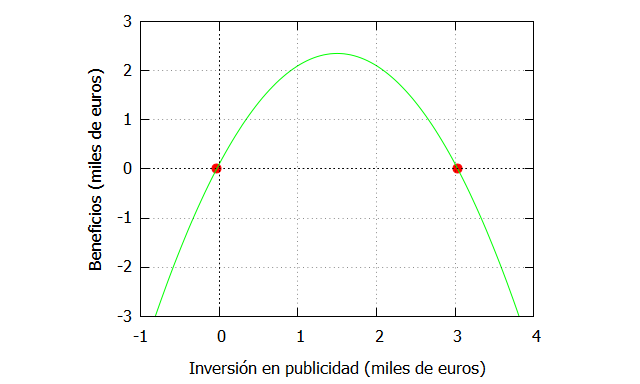
Emplearemos la misma función que en los ejemplos anteriores, donde se relaciona la inversión en publicidad con los beneficios.

f_ceronegativo:ev(funcion,x=-0.03297097167558977), numer; f_ceropositivo:ev(funcion,x=3.03297097167559), numer; plot2d([[discrete, [[-0.0329709716755897,f_ceronegativo], [3.03297097167559, f_ceropositivo]]], funcion],[x,-1,4],[y,-3,3], [xlabel, «Inversión en publicidad (miles de euros)»], [ylabel, «Beneficios (miles de euros)»], [style, points, lines], [color, red, green], [legend, false]);

Método de Newton

(1) Objetivo: Aproximarse numéricamente a la solución p de una función , tal que

(2) Condiciones: La función debe ser continua y dos veces diferenciable en el intervalo considerado.

(3) Descripción rápida: Partimos del primer polinomio de Taylor para  expandido alrededor de  y evaluado en  . Suponemos que es una buena aproximación a , es decir, que la semilla inicial está relativamente cerca de la solución. Cuando , entonces, obviando el término de error de la serie de Taylor:

A partir de esa fórmula podemos construir la sucesión donde:

(4) Convergencia: Un criterio suficiente (pero no necesario) para que lo haga es que:

Si se cumple la fórmula anterior cuando está en un intervalo alrededor de la raíz entonces la solución converge en cualquier punto de ese intervalo. La convergencia es no lineal (cuadrática), y esta es una de las razones por las que es uno de los procedimientos más empleados.

(5) Estimación del error: Hay diversas opciones, aunque una de las más recomendables es el error relativo:

Implementación en Maxima

Vamos a implementar el algoritmo partiendo de 3 semillas diferentes, para ver que en función de la elección de ellas nos puede llevar a una de las dos soluciones posibles.  Para ello, empleamos un bucle con 10 iteraciones, tomando como semillas: 3, 0.1 y 8. Esto hace que evaluemos 3 funciones diferentes (f1, f2, f3) a la hora de analizar su convergencia.

f1(i):= -x1[i]^2+3*x1[i]+0.1; derivada_f1(i):=-(2*x1[i])+3; x1[0]:3; for i:1 thru 10 do( x1[i]:x1[i-1]-(f1(i-1)/derivada_f1(i-1))); f2(i):= -x2[i]^2+3*x2[i]+0.1; derivada_f2(i):=-(2*x2[i])+3; x2[0]:0.2; for i:1 thru 10 do( x2[i]:x2[i-1]-(f2(i-1)/derivada_f2(i-1))); f3(i):= -x3[i]^2+3*x3[i]+0.1; derivada_f3(i):=-(2*x3[i])+3; x3[0]:8; for i:1 thru 10 do( x3[i]:x3[i-1]-(f3(i-1)/derivada_f3(i-1))); datos: makelist([i,»Iteración»,x1[i],f1(i-1), x2[i],f2(i-1),     x3[i], f3(i-1)], i, 1,10); matriz_resultados:apply(matrix,datos);

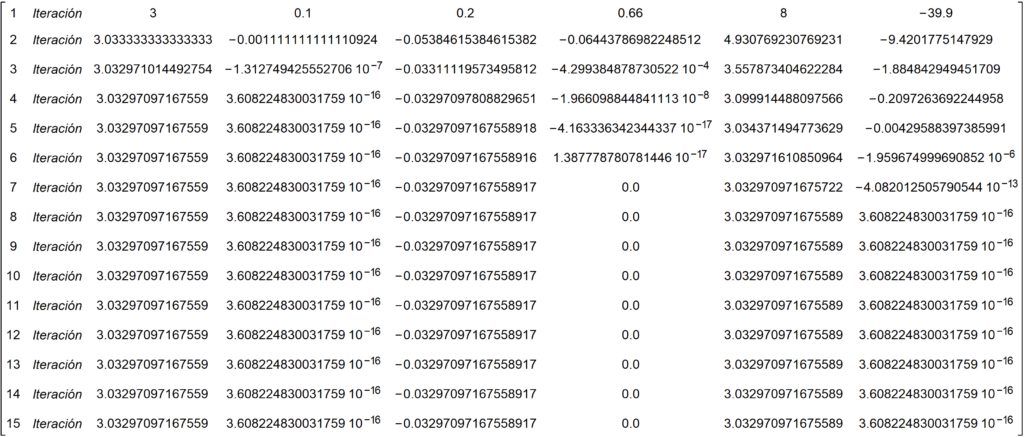
Le hemos dicho al programa que nos retorne en el output siguiente:

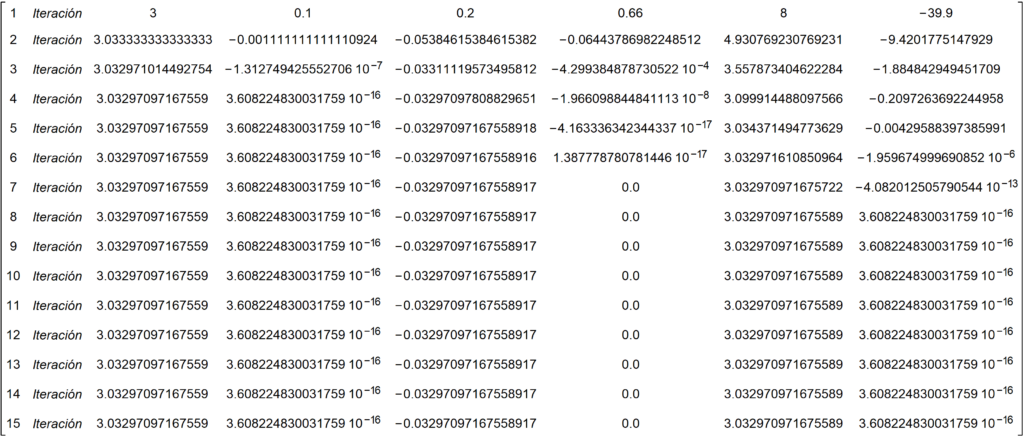
El método converge bastante rápido, incluso cuando la semilla se aleja de la raíz, y como puede observarse en función de la elección de la semilla converge hacia una de las dos soluciones.

Criterio de parada

Al igual que hicimos en el método de la bisección, podemos estipular que nos baste con una tolerancia de error, es decir, pedirle al programa que pare las iteraciones cuando se cumpla una condición determinada, por ejemplo, que el error relativo sea menor que una cota que fijemos. De este modo, si fijamos que el error relativo sea como máximo 0.0001:

f1(i):= -p[i]^2+3*p[i]+0.1; derivada_f1(i):=-(2*p[i])+3; p[0]:8; for i:1 while Error_rel[i]>0.0001 do( p[i]:p[i-1]-(f1(i-1)/derivada_f1(i-1)), Error_abs[i]:abs(p[i]-p[i-1]), Error_rel[i]: Error_abs[i]/abs(p[i]),     print(i,p[i],Error_rel[i]));

Le hemos dicho al programa que fije un error relativo mayor que 0.0001, por lo que parará en esa iteración, y de esta manera sabremos que en la siguiente iteración el error relativo estará por debajo de esa cota. Si ejecutamos esas instrucciones en Maxima vemos que para en la iteración número 5, por lo que incluso con semillas alejadas de la raíz la convergencia puede ser muy rápida.

Conclusión

En este post hemos explicado brevemente en qué consiste el método de Newton, un algoritmo muy empleado en diversas aplicaciones estadísticas, como para obtener los estimadores que minimizan una función de error (hacen que su derivada sea cero, por lo que es realmente obtener la aproximación numérica a la raíz de una función). El método de Newton tiene, además, diversas variantes que comentaremos en futuras entradas.