INTERPOLACIÓN (I): POLINOMIO DE LAGRANGE

Para los alumnos de marketing es tarea fundamental conocer cómo se pueden hacer predicciones a partir de datos empíricos. Vamos a explicar en una serie de posts diversas formas de hacerlo, comenzando con una de las más conocidas, el polinomio de Lagrange. Lo haremos, como siempre, desde el punto de vista práctico, y siguiendo a Burden, Faires & Burden (2017). El objetivo es, asimismo, que los estudiantes sean autónomos y sepan programar este tipo de métodos, y para ello proveeremos de códigos de Maxima.

Datos de partida

Imaginemos que partimos de los siguientes datos empíricos:

x	f(x)
1	1
3	2
4	4
6	5
7	7
8	9
9	2
10	10
11	10
12	10

Estos datos relacionan la cantidad de empleados utilizados en un gran supermercado (x) con la saltisfacción del cliente $y=f(x)$ . La satisfacción del cliente se mide en una escala de 0 a 10, donde 0 es el valor mínimo y 10 el valor máximo.

Lo más indicado es proceder primeramente con una representación gráfica de los datos. Recordemos que el problema aquí es que conocemos los datos pero no conocemos cómo se relacionan, es decir, sabemos que existe una función $f(x)$ , que depende obviamente de x, pero no sabemos cómo es.

En Maxima podemos inspeccionar esos datos de la siguiente forma:

x_:[1,3,4,6,7,8,9,10,11,12]; fx_:[1,2,4,5,7,9,2,10,10,10]; plot2d([discrete, x_, fx_], [x,0,15],[y,0,10], [style, points], [color,green], [xlabel, «Número de empleados»], [ylabel, «Satisfacción del cliente»], [legend, false]);

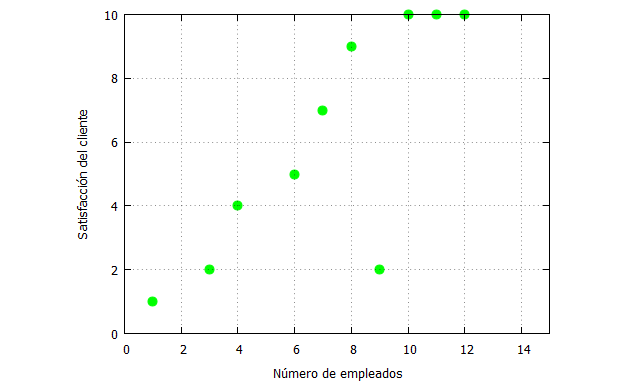
Vemos que en principio existe una asociación positiva entre ambas variables, pero nos interesaría saber cuál será el nivel de satisfacción si contamos con empleados que no estaban en los datos originales. Además, esa relación no está muy claro que sea lineal, al menos no en todo el dominio de la función, por lo que necesitamos recurrir a herramientas matemáticas para tratar de ser más precisos en el análisis y tener menos riesgo en la toma de decisiones.

Método de Lagrange

(1) Objetivo: Aproximarse numéricamente a la función $f(x)$ , de la que conocemos sólo ciertos datos $(x_{i},f(x_{i}))$ por medio de un polinomio que «pase» por los i puntos conocidos.

(2) Condiciones: La función $f(x)$ debe ser continua en el intervalo $[a,b]$ considerado.

(3) Descripción rápida: Partimos de dos puntos $(x_{0},f(x_{0}))$ y $(x_{1},f(x_{1}))$ . Definimos las funciones:

$L_{0}(x)=\frac{x-x_{1}}{x_{0}-x_{1}}$

$L_{1}(x)=\frac{x-x_{0}}{x_{1}-x_{0}}$

El polinomio de interpolación de Lagrange $P(x)$ entre esos dos puntos es:

$P(x)=L_{0}(x)f(x_{0})+L_{1}(x)f(x_{1})= \frac{x-x_{1}}{x_{0}-x_{1}}f(x_{0})+\frac{x-x_{0}}{x_{1}-x_{0}}f(x_{1})$

Por lo que tendremos un polinomio de grado m=1 que pasa por $(x_{0},x_{1})$ .Es decir, para n puntos vamos a considerar un polinomio de grado m=n-1

De forma más compacta y general:

$P(x)=\sum_{j=0}^{m}f(x_{j})L_{j}(x)$

$L_{j}(x)=\prod_{i=0,i\neq j}^{m}\frac{x-x_{i}}{x_{j}-x_{i}}$

Por ejemplo, para n=3 puntos, entonces el polinomio sería de orden m=2, y deberíamos definir n=3 sumandos en $P(x)$ , donde cada $L_{j}(x)$ será la múltiplicación de m=2 términos. Es decir:

$L_{0}(x)=\frac{x-x_{1}}{x_{0}-x_{1}}\frac{x-x_{2}}{x_{0}-x_{2}}$

$L_{1}(x)=\frac{x-x_{0}}{x_{1}-x_{0}}\frac{x-x_{2}}{x_{1}-x_{2}}$

$L_{2}(x)=\frac{x-x_{0}}{x_{2}-x_{0}}\frac{x-x_{1}}{x_{2}-x_{1}}$

$P(x)=\sum_{j=0}^{2}f(x_{j})L_{j}(x)$

(4) Estimación del error: Para estimar el error $E(x)$ necesitamos conocer la forma de la función real:

$E(x)=f(x)-P(x)=\frac{f^{n}(\xi (x))}{(n)!}\prod_{j=0}^{m}(x-x{j})$

donde $\xi(x)$ es un número que está dentro del intervalo de datos considerado. De este modo, únicamente si conocemos $f(x)$ podremos derivarla n veces. Por tanto, si tenemos n=3 puntos habrá que hacer n=3 derivadas para obtener el error de un polinomio de orden m=2. En la mayoría de los casos no conoceremos esa función, ya que ese desconocimiento precisamente es la causa por la cual necesitamos interpolar. No obstante, si conocemos la función, podemos calcular una cota de error máximo para cualquier punto contenido dentro del intervalo considerado.

Implementación en Maxima

Vamos a realizar nuestra primera estimación en Maxima. Supongamos que queremos aproximarnos a un valor que desconocemos, cuando el número de empleados es 2. Para ello tenemos diversas opciones. La primera es considerar sólo un número de puntos cercano al objetivo, y la segunda considerar toda la información disponible. Ambas tienen ventajas e inconvenientes. Comencemos con la primera opción, calculando un polinomio de Lagrange de orden 2 que pase por los 3 primeros puntos de nuestros datos.

p(x):=(x-x1)*(x-x2)*fx0/((x0-x1)*(x0-x2))+ (x-x0)*(x-x2)*fx1/((x1-x0)*(x1-x2))+ (x-x0)*(x-x1)*fx2/((x2-x0)*(x2-x1)); expand(p(x)); x0:1; x1:3; x2:4; fx0:1; fx1:2; fx2:4; solucion1: expand(p(x)); f_solucion1: ev(solucion1,x=2); x_:[1,3,4,6,7,8,9,10,11,12]; fx_:[1,2,4,5,7,9,2,10,10,10]; x_solucion1:2; plot2d([[discrete, x_, fx_], [discrete, [[x_solucion1,f_solucion1]]],solucion1], [x,0,15],[y,0,10], [style, points, points, lines], [color,green, red, orange], [xlabel, «Número de empleados»], [ylabel, «Satisfacción del cliente»], [legend, false]);

El polinomio resultante es:

$P(x)=\frac{x^{2}}{2}-\frac{3x}{2}+2$

que nos indica que la satisfación del cliente será:

$f(x)=1$

Y su representación gráfica:

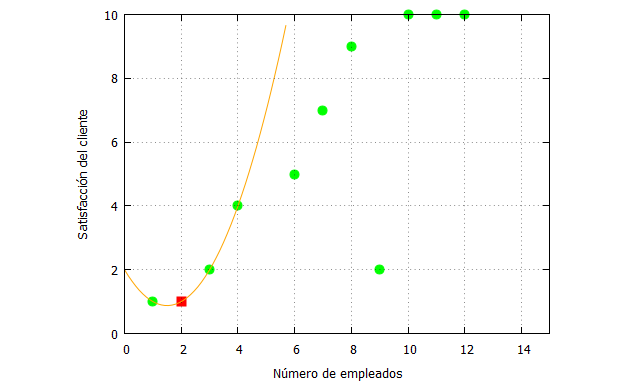Vamos a ir comprobando qué ocurriría con la estimación a medida que incorporamos nueva información en el polinomio de Lagrange.

Si ahora usamos n=4 puntos:

kill (all); p(x):=(x-x1)*(x-x2)*(x-x3)*fx0/((x0-x1)*(x0-x2)*(x0-x3))+ (x-x0)*(x-x2)*(x-x3)*fx1/((x1-x0)*(x1-x2)*(x1-x3))+ (x-x0)*(x-x1)*(x-x3)*fx2/((x2-x0)*(x2-x1)*(x2-x3))+ (x-x0)*(x-x1)*(x-x2)*fx3/((x3-x0)*(x3-x1)*(x3-x2)); expand(p(x)); x0:1; x1:3; x2:4; x3:6; fx0:1; fx1:2; fx2:4; fx3:5; solucion1: expand(p(x)); f_solucion1: ev(solucion1,x=2); x_:[1,3,4,6,7,8,9,10,11,12]; fx_:[1,2,4,5,7,9,2,10,10,10]; x_solucion1:2; plot2d([[discrete, x_, fx_], [discrete, [[x_solucion1,f_solucion1]]],solucion1], [x,0,15],[y,0,10], [style, points, points, lines], [color,green, red, orange], [xlabel, «Número de empleados»], [ylabel, «Satisfacción del cliente»], [legend, false]);

El polinomio resultante es:

$P(x)=-\frac{x^{3}}{5}+\frac{21x^{2}}{10}-\frac{53x}{10}+\frac{22}{5}$

que nos indica que la satisfación del cliente será:

$f(x)=0.6$

Y su representación gráfica:

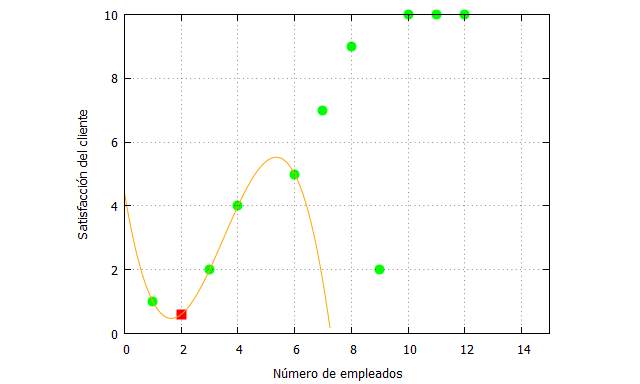Vemos como ahora la estimación cambia considerablemente al cambiar también la forma de la función de interpolación.

Pero si empleamos todos los puntos disponibles:

p(x):=(x-x1)*(x-x2)*(x-x3)*(x-x4)*(x-x5)*(x-x6)*(x-x7)*(x-x8)*(x-x9)*fx0/ ((x0-x1)*(x0-x2)*(x0-x3)*(x0-x4)*(x0-x5)*(x0-x6)*(x0-x7)*(x0-x8)*(x0-x9))+ (x-x0)*(x-x2)*(x-x3)*(x-x4)*(x-x5)*(x-x6)*(x-x7)*(x-x8)*(x-x9)*fx1/ ((x1-x0)*(x1-x2)*(x1-x3)*(x1-x4)*(x1-x5)*(x1-x6)*(x1-x7)*(x1-x8)*(x1-x9))+ (x-x0)*(x-x1)*(x-x3)*(x-x4)*(x-x5)*(x-x6)*(x-x7)*(x-x8)*(x-x9)*fx2/ ((x2-x0)*(x2-x1)*(x2-x3)*(x2-x4)*(x2-x5)*(x2-x6)*(x2-x7)*(x2-x8)*(x2-x9))+ (x-x0)*(x-x1)*(x-x2)*(x-x4)*(x-x5)*(x-x6)*(x-x7)*(x-x8)*(x-x9)*fx3/ ((x3-x0)*(x3-x1)*(x3-x2)*(x3-x4)*(x3-x5)*(x3-x6)*(x3-x7)*(x3-x8)*(x3-x9))+ (x-x0)*(x-x1)*(x-x2)*(x-x3)*(x-x5)*(x-x6)*(x-x7)*(x-x8)*(x-x9)*fx4/ ((x4-x0)*(x4-x1)*(x4-x2)*(x4-x3)*(x4-x5)*(x4-x6)*(x4-x7)*(x4-x8)*(x4-x9))+ (x-x0)*(x-x1)*(x-x2)*(x-x3)*(x-x4)*(x-x6)*(x-x7)*(x-x8)*(x-x9)*fx5/ ((x5-x0)*(x5-x1)*(x5-x2)*(x5-x3)*(x5-x4)*(x5-x6)*(x5-x7)*(x5-x8)*(x5-x9))+ (x-x0)*(x-x1)*(x-x2)*(x-x3)*(x-x4)*(x-x5)*(x-x7)*(x-x8)*(x-x9)*fx6/ ((x6-x0)*(x6-x1)*(x6-x2)*(x6-x3)*(x6-x4)*(x6-x5)*(x6-x7)*(x6-x8)*(x6-x9))+ (x-x0)*(x-x1)*(x-x2)*(x-x3)*(x-x4)*(x-x5)*(x-x6)*(x-x8)*(x-x9)*fx7/ ((x7-x0)*(x7-x1)*(x7-x2)*(x7-x3)*(x7-x4)*(x7-x5)*(x7-x6)*(x7-x8)*(x7-x9))+ (x-x0)*(x-x1)*(x-x2)*(x-x3)*(x-x4)*(x-x5)*(x-x6)*(x-x7)*(x-x9)*fx8/ ((x8-x0)*(x8-x1)*(x8-x2)*(x8-x3)*(x8-x4)*(x8-x5)*(x8-x6)*(x8-x7)*(x8-x9))+ (x-x0)*(x-x1)*(x-x2)*(x-x3)*(x-x4)*(x-x5)*(x-x6)*(x-x7)*(x-x8)*fx9/ ((x9-x0)*(x9-x1)*(x9-x2)*(x9-x3)*(x9-x4)*(x9-x5)*(x9-x6)*(x9-x7)*(x9-x8)) ; x0:1; x1:3; x2:4; x3:6; x4:7; x5:8; x6:9; x7:10; x8:11; x9:12; fx0:1; fx1:2; fx2:4; fx3:5; fx4:7; fx5:9; fx6:2; fx7:10; fx8:10; fx9:10; solucion1: expand(p(x)); f_solucion1: ev(solucion1,x=2);

El polinomio resultante es de noveno grado, y cuando lo evaluamos en x=2 nos indica que la satisfación del cliente es:

$f(x)=1718.6$

Y su representación gráfica:

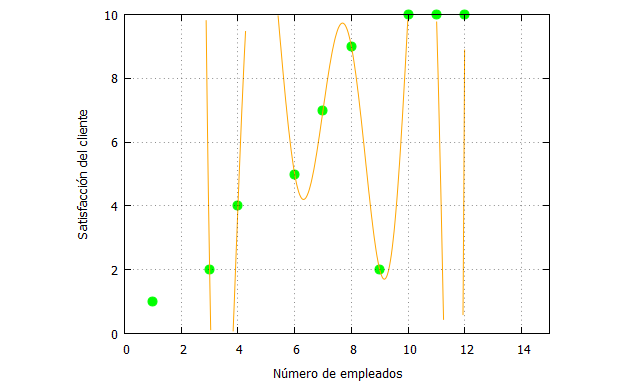
Rápidamente se puede ver el «disparate» de esta interpolación que nos lleva un resultado absolutamente sin sentido en el contexto de los datos.

Aunque en posteriores posts de esta serie comentaremos con mayor profundidad el concepto de sobreajuste, lo que ha sucedido es precisamente un ajuste innecesario de todos los puntos, que indica que hemos modelado no sólo la «señal» subyacente, sino el «ruido». Ambos conceptos, señal y ruido, son fundamentales para entender la naturaleza de las estimaciones, inferencias e interpolaciones.

Una vez que ya hemos practicado con la programación «a mano», podemos pedirle a Maxima que nos «ayude» con la interpolación usando una de sus funciones propias del programa, lo que resulta mucho más sencillo:

kill (all); datos:[[1,1],[3,2],[4,4],[6,5],[7,7], [8,9],[9,2],[10,10],[11,10],[12,10]]; load (interpol); lagrange(datos);

Que nos da la solución anterior con mucho menos esfuerzo de programación.

Conclusión

En este post hemos explicado brevemente en qué consiste el método de los polinomios de Lagrange para interpolar una función. Antes de su aplicación, hay que estudiar previamente la naturaleza de los datos, hacer inspecciones gráficas, y valorar en qué medida son necesarios escoger todos los datos, o sólo aquellos que estén en la vecindad del punto que se quiere interpolar.

Aprenderemos a evaluar en qué situaciones conviene su implementación o es mejor realizar ajustes estadísticos a los datos (como por mínimos cuadrados ordinarios), que nos permitan minimizar y analizar mejor la señal, pese a que podamos perder precisión para algún punto específico que queramos predecir.

Category: METODOLOGÍA DE INVESTIGACIÓN

4 comentarios en «INTERPOLACIÓN (I): POLINOMIO DE LAGRANGE»