Una manera de simplificar los cálculos globales del método de Lagrange es emplear la propuesta de Neville, que genera los polinomios de interpolación de forma recursiva en varias etapas de cálculo.
Datos de partida
Usaremos los mismos datos que en el método de Lagrange:
| x | f(x) |
| 1 | 1 |
| 3 | 2 |
| 4 | 4 |
| 6 | 5 |
| 7 | 7 |
| 8 | 9 |
| 9 | 2 |
| 10 | 10 |
| 11 | 10 |
| 12 | 10 |
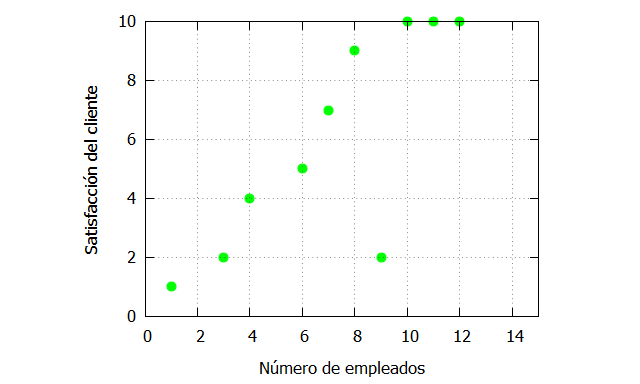
Estos datos relacionan la cantidad de empleados utilizados en un gran supermercado (x) con la saltisfacción del cliente . La satisfacción del cliente se mide en una escala de 0 a 10, donde 0 es el valor mínimo y 10 el valor máximo.
| x_:[1,3,4,6,7,8,9,10,11,12]; fx_:[1,2,4,5,7,9,2,10,10,10]; plot2d([discrete, x_, fx_], [x,0,15],[y,0,10], [style, points], [color,green], [xlabel, “Número de empleados”], [ylabel, “Satisfacción del cliente”], [legend, false]); |
Método de Neville
(1) Objetivo: Aproximarse numéricamente a la función , de la que conocemos sólo ciertos datos por medio de un polinomio que “pase” por los i puntos conocidos.
(2) Condiciones: La función debe ser continua en el intervalo
considerado.
(3) Descripción rápida: Partimos de la serie de datos y definimos
los elementos de la tabla de interpolación:
Básicamente se trata de ir interpolando entre pares de valoremos consecutivos en la primera columna, luego entre pares de valores que se llevan dos filas en la segunda, tres filas en la tercera, etc.
Así, construimos una tabla que es una matriz de n filas por n columnas que es triangular y cuyo último elemento de la diagonal coincide con el valor del polinomio de Lagrange entre todos los puntos considerados.
(4) Estimación del error: Podemos emplear el mismo sistema que para el método de Lagrange
Implementación en Maxima
Vamos a realizar nuestra estimación en Maxima. Supongamos, como en el caso del método de Lagrange, que queremos aproximarnos a un valor que desconocemos, cuando el número de empleados es 2. Para ello vamos a coger los 3 primeros puntos, con la programación siguiente:
| X_: matrix([1,3,4]); X_t:transpose(X_); FX_:matrix([1,2,4]); FX_t:transpose(FX_); [n,m] : matrix_size (FX_t) ; Neville1: zeromatrix(n,m); Neville2: zeromatrix(n,m); Neville3 : zeromatrix(n,m); x:2; for k:1 thru n do ( Neville1[k,1]:FX_t[k,1], for k:2 thru n do ( Neville2[k,1]:(((x-X_t[k-1,1])*FX_t[k,1])-(x-X_t[k,1])*FX_t[k-1,1])/(X_t[k,1]-X_t[k-1]), for k:3 thru n do ( Neville3[k,1]:((((x-X_t[k-2,1])*Neville2[k,1]))-((x-X_t[k,1])*Neville2[k-1,1]))/(X_t[k,1]-X_t[k-2,1])))); ResultadosNeville:addcol(X_t,Neville1,Neville2,Neville3); |
La tabla resultante (en forma de matriz) es:
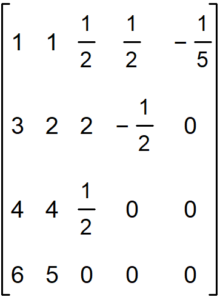
donde en la primera columna tenemos los valores de y en las 3 restantes los valores computados por el procedimiento de Neville. Es decir los valores de los puntos más la tabla de Neville. Nótese que la columna dos son las imágenes
de la primera columna.
Por tanto, tenemos que, la estimación es 1 (el último elemento de la diagonal de las columnas de Neville), que coincide con el resultado calculado por el método de Lagrange.
En Maxima, lo que hemos hecho es crear una matriz de 3×3 (ya que usamos 3 puntos para la interporlación de x=2) con ceros a la que vamos a ir añadiendo en cada columna los valores calculados por el procedimiento de Neville.
Conclusión
El método de Neville realiza una interpolación iterada de manera secuencial, usando las estimaciones previas del polinomio de Lagrange, simplificando el proceso de cálculo.
