El polinomio de Lagrange se puede obtener también por medio de un método sencillo que emplea diferencias divididas de las imágenes con respecto a x. Este método también se conoce como “diferencias divididas de Newton”. Seguiremos a Burden, Faires & Burden (2017), y lo enfocaremos, como siempre, de manera simplificada.
Datos de partida
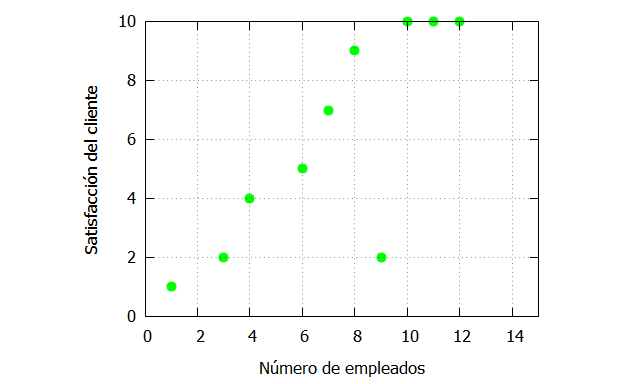
Usaremos los mismos datos que en el método de Lagrange:
| x | f(x) |
| 1 | 1 |
| 3 | 2 |
| 4 | 4 |
| 6 | 5 |
| 7 | 7 |
| 8 | 9 |
| 9 | 2 |
| 10 | 10 |
| 11 | 10 |
| 12 | 10 |
Estos datos relacionan la cantidad de empleados utilizados en un gran supermercado (x) con la satisfacción del cliente . La satisfacción del cliente se mide en una escala de 0 a 10, donde 0 es el valor mínimo y 10 el valor máximo.
| x_:[1,3,4,6,7,8,9,10,11,12]; fx_:[1,2,4,5,7,9,2,10,10,10]; plot2d([discrete, x_, fx_], [x,0,15],[y,0,10], [style, points], [color,green], [xlabel, “Número de empleados”], [ylabel, “Satisfacción del cliente”], [legend, false]); |
Método de diferencias divididas
(1) Objetivo: Aproximarse numéricamente a la función , de la que conocemos sólo ciertos datos por medio de un polinomio que “pase” por los i puntos conocidos.
(2) Condiciones: La función debe ser continua en el intervalo
considerado.
(3) Descripción rápida: Partimos de la serie de datos y definimos la primera diferencia dividida como
Si implementamos ese cálculo de manera recursiva llegamos a la fórmula general:
Así, construimos una tabla de n-1 diferencias divididas a partir de las cuales podemos hallar el polinimio de Lagrange:
(4) Estimación del error: Podemos emplear el mismo sistema que para el método de Lagrange
Implementación en Maxima
Vamos a realizar nuestra estimación en Maxima. Supongamos, como en el caso del método de Lagrange, que queremos aproximarnos a un valor que desconocemos, cuando el número de empleados es 2. Para ello vamos a coger los 4 primeros puntos, con la programación siguiente:
| x_:[1,3,4,6]; fx:[1,2,4,5]; valores: transpose(matrix(x_)); imagenes: transpose(matrix(fx)); [n,m]:matrix_size (valores); funcion__1: zeromatrix(n,m); for k:1 thru n-1 do (funcion__1[k,1]: (imagenes[k+1,1]-imagenes[k,1])/(valores[k+1,1]-valores[k,1]))$ print(funcion__1); funcion__2: zeromatrix(n,m); for k:1 thru n-2 do (funcion__2[k,1]: (funcion__1[k+1,1]-funcion__1[k,1])/((valores[k+2,1]-valores[k,1])))$ print(funcion__2); funcion__3: zeromatrix(n,m); for k:1 thru n-3 do (funcion__3[k,1]: (funcion__2[k+1,1]-funcion__2[k,1])/((valores[k+3,1]-valores[k,1])))$ print(funcion__3); matriztotal: addcol(valores,imagenes,funcion__1,funcion__2, funcion__3); p3:matriztotal[1,2]+((x-matriztotal[1,1])*matriztotal[1,3])+((x-matriztotal[1,1])*(x-matriztotal[2,1])*matriztotal[1,4]) +((x-matriztotal[1,1])*(x-matriztotal[2,1])*(x-matriztotal[3,1])*matriztotal[1,5]); |
La tabla resultante (en forma de matriz) es:
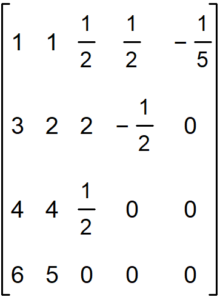
donde en la primera columna tenemos los valores de en la segunda los valores de
y en las 3 restantes los valores computados por el procedimiento de Newton.
Por tanto, podemos construir el polinomio de Lagrange a partir de estos resultados, que nos lo da la parte de código ya implementado:
| p3:matriztotal[1,2]+((x-matriztotal[1,1])*matriztotal[1,3])+((x-matriztotal[1,1])*(x-matriztotal[2,1])*matriztotal[1,4]) +((x-matriztotal[1,1])*(x-matriztotal[2,1])*(x-matriztotal[3,1])*matriztotal[1,5]); |
El polinomio resultante es:
Que como vemos es un polinomio de orden 3, ya que hemos cogido 4 puntos para la interpolación. Si ahora evaluamos el polinomio en el punto de interés x=2:
| solucion:ev(p3,x=2); |
Obtenemos el resultado de:
que es exactamente lo mismo que lográbamos con la implementación directa de la fórmula del polinomio de Lagrange.
Diferencias hacia atrás
La obtención del polinomio de Lagrange puede lograrse cambiando la forma de recorrer la matriz de diferencias devididas. En lugar de hacerlo desde lo hacemos desde
. Gráficamente quizá se entiende mejor: en verde el método hacia adelante y en rojo el método hacia atrás.
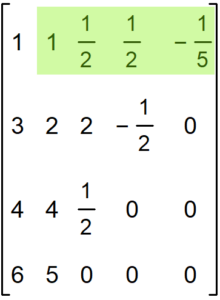
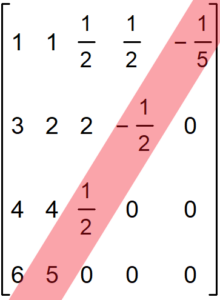
Los resultados son idénticos, y lo podemos comprobar con el siguiente código:
| p3_atras:matriztotal[4,2]+((x-matriztotal[4,1])*matriztotal[3,3])+((x-matriztotal[4,1])*(x-matriztotal[3,1])*matriztotal[2,4]) +((x-matriztotal[4,1])*(x-matriztotal[3,1])*(x-matriztotal[2,1])*matriztotal[1,5]), ratsimp; |
Evidentemente, tenemos que tener cuidado de comenzar a contar las “x” desde el final en lugar que desde el principio.
Nodos con igual espaciado
Cuando los puntos (nodos) se pueden ordenar con igual espaciado, podemos también obtener el polinomio de Lagrange a través de la siguiente fórmula:
donde n es el orden del polinomio, y son las diferencias divididas entre las imágenes consecutivas. Además,
donde
es el dato para el que se quiere estimar su imagen y
es el dato de partida elegido para la interpolación. Finalmente
es la holgura del espaciado entre los datos.
En Maxima, podemos implementar el procedimiento anterior intentando inferir el valor de x=5 cuando se cogen los nodos equiespaciados [4,6,8,10]. El valor de la fórmula anterior quedaría así
| x_:[4,6,8,10]; fx:[4,5,9,10]; valores: transpose(matrix(x_)); imagenes: transpose(matrix(fx)); [n,m]:matrix_size (valores); funcion__1: zeromatrix(n,m); for k:1 thru n-1 do (funcion__1[k,1]: imagenes[k+1,1]-imagenes[k,1])$ print(funcion__1); funcion__2: zeromatrix(n,m); for k:1 thru n-2 do (funcion__2[k,1]: funcion__1[k+1,1]-funcion__1[k,1])$ print(funcion__2); funcion__3: zeromatrix(n,m); for k:1 thru n-3 do (funcion__3[k,1]: funcion__2[k+1,1]-funcion__2[k,1])$ print(funcion__3); matriztotal: addcol(valores,imagenes,funcion__1,funcion__2, funcion__3); xs: 5; xp:4; h:2; s:(xs-xp)/h; p3_equiespaciado:matriztotal[1,2]+(s*matriztotal[1,3])+((s*(s-1)/2)*matriztotal[1,4]) +(s*(s-1)*(s-2)/6)*matriztotal[1,5]; |
Que nos da un valor:
Conclusión
El método de diferencias divididas proporciona una forma simplificada de obtener el polinomio de Lagrange. Sin embargo, está sujeto a las mismas limitaciones, es decir, hemos de ser muy cuidadosos a la hora de elegir los nodos de interpolación.
