INTERPOLACIÓN (IV): MÉTODO DE SPLINE CÚBICO

Los métodos de interpolación vistos hasta ahora no permitían aproximar a la función por tramos. El método de spline sí que lo puede hacer, y es muy potente para conseguir buenos resultados en cualquier tipo de análisis de datos. Seguiremos a Burden, Faires & Burden (2017), y lo enfocaremos, como siempre, de manera simplificada.

Datos de partida

Usaremos los mismos datos que en el método de Lagrange:

x	f(x)
1	1
3	2
4	4
6	5
7	7
8	9
9	2
10	10
11	10
12	10

Estos datos relacionan la cantidad de empleados utilizados en un gran supermercado (x) con la saltisfacción del cliente $y=f(x)$ . La satisfacción del cliente se mide en una escala de 0 a 10, donde 0 es el valor mínimo y 10 el valor máximo.

x_:[1,3,4,6,7,8,9,10,11,12]; fx_:[1,2,4,5,7,9,2,10,10,10]; plot2d([discrete, x_, fx_], [x,0,15],[y,0,10], [style, points], [color,green], [xlabel, «Número de empleados»], [ylabel, «Satisfacción del cliente»], [legend, false]);

Método de spline cúbico

(1) Objetivo: Aproximarse numéricamente a la función $f(x)$ , de la que conocemos sólo ciertos datos por medio de varios polinomios que pasen por los i puntos conocidos, es decir, calcularemos polinomios por tramos de datos. Emplearemos, además, splines cúbicos, es decir, polinomios de orden 3.

(2) Condiciones: La función $f(x)$ debe ser continua en el intervalo $[a,b]$ considerado y además tiene que ser doblemente diferenciable.

(3) Descripción rápida: Partimos de la serie de datos $(x_{i},f(x_{i}))$ , los cuales es conveniente ordenar de manera creciente por los nodos $x_{i}$ , y escogemos los j subintervalos para los cuales vamos a calcular splines $S_{j}(x)$ .

La condiciones que deben satisfacerse son las siguientes:

a) $S_{j}(x)$ son los j polinomios que se calculan para los i=j+1 nodos.

b) $S_{j}(x_{j})=f(x_{j})$ y $S_{j}(x_{j+1})=f(x_{j+1})$ para cada j. Es decir, el spline cúbico debe pasar por todas las imágenes de los datos, y esto hace que dos splines consecutivos pasen por un nodo común, por lo que al evaluar ambos splines en el mismo punto el resultado deba ser el mismo.

c) $S'_{j+1}(x_{j+1})=S'_{j}(x_{j+1})$ y $S''_{j+1}(x_{j+1})=S''_{j}(x_{j+1})$ para cada j=1…n-2. No sólo las evaluaciones de los splines, sino también sus derivadas primera y segunda deben coincidir en los nodos de conexión.

d) Si el spline es natural (frontera libre), entonces: $S''(x_{1})=S''(x_{n})=0$

Los splines de frontera condicionada no los vamos a comentar ya que es necesario conocer los valores de la derivada de la función original en los extremos, algo de lo que carecemos, debido a que sólo tenemos un conjunto de datos brutos y sus imágenes.

Estas condiciones suponen unas restricciones en la resolución de un sistema de ecuaciones con 4xj incógnitas. Es decir, 4 incógnitas por cada spline calculado. Así, para n=3 puntos obtendríamos j=2 splines cúbicos, de la forma:

$S_{1}(x)=a_{1}+b_{1}(x-1)+c_{1}(x-1)^{2}+d_{1}(x-1)^{3}$

$S_{2}(x)=a_{2}+b_{2}(x-3)+c_{2}(x-3)^{2}+d_{2}(x-3)^{3}$

Ahora tenemos que determinar esas constantes usando las restricciones comentadas anteriormente.

b) $a_{1}=f(x_{1})$ , $f(x_{2})=a_{1}+2b_{1}+4c_{1}+8d_{1}$ , $f(x_{2})=a_{2}$ , $a_{2}+b_{2}+c_{2}+d_{2}=f(x_{3})$

c) $S'_{1}(x_{2})=S'_{2}(x_{2})$ , por lo que $b_{1}+4c_{1}+12d_{1}=b_{2}$

y $S''_{1}(x_{2})=S''_{2}(x_{2})$ , por lo que $2c_{1}+12d_{1}=2c_{2}$

d) $S''_{1}(x_{1})=0$ , por lo que $2c_{1}=0$

y $S''_{1}(x_{3})=0$ , por lo que $2c_{2}+6d_{2}=0$

Ya sólo queda resolver el sistema de ecuaciones anterior, es decir, y considerando los nodos [1,3,4] e imágenes [1,2,4]:

$\begin{matrix} a_{1}=1 \\a_{1}+2b_{1}+4c_{1}+8d_{1}=2 \\ a_{2}=2\\a_{2}+b_{2}+c_{2}+d{2}=4 \\b_{1}+4c_{1}+12d_{1}=b_{2} \\2c_{1}+12d_{1}=2c_{2} \\ 2c_{1}=0\\2c_{2}+6d_{2}=0 \end{matrix}$

Implementación en Maxima

Vamos a realizar nuestra estimación en Maxima. Supongamos, como en el caso del método de Lagrange, que queremos aproximarnos a un valor que desconocemos, cuando el número de empleados es 2. Para ello vamos a coger los 3 primeros puntos, con la programación siguiente:

x_:[1,3,4]; fx:[1,2,4]; S1: a1+b1*(x-x_[1])+c1*(x-x_[1])^2+d1*(x-x_[1])^3; S2: a2+b2*(x-x_[2])+c2*(x-x_[2])^2+d2*(x-x_[2])^3; fx1:ev(S1,x=x_[1]); fx2:ev(S1,x=x_[2]); fx2_:ev(S2,x=x_[2]); fx3:ev(S2,x=x_[3]); S1prima: diff(S1,x); S1prima_ev:ev(S1prima,x=x_[2]); S2prima: diff(S2,x); S2prima_ev:ev(S2prima,x=x_[2]); S1primaprima: diff(S1prima,x); S1primaprima_ev:ev(S1primaprima,x=x_[2]); S2primaprima: diff(S2prima,x); S2primaprima_ev:ev(S2primaprima,x=x_[2]); S1primaprimainicio_ev:ev(S1primaprima,x=x_[1]); S2primaprimafin_ev:ev(S2primaprima,x=x_[3]); e1: fx1-fx[1]; e2: fx2-fx[2]; e3: fx2_-fx[2]; e4:fx3-fx[3]; e5:S1prima_ev-S2prima_ev; e6:S1primaprima_ev-S2primaprima_ev; e7:S1primaprimainicio_ev-0; e8: S2primaprimafin_ev-0; algsys ([e1, e2, e3, e4,e5,e6,e7,e8], [a1,b1,c1,d1,a2,b2,c2,d2]);

Aunque a priori parece un código algo complejo, lo cierto es que sigue paso a paso el algoritmo que deviene de las restricciones planteadas. Para formular el sistema de ecuaciones a resolver, hay que recordar que debemos escribir esas ecuaciones en Maxima de la forma x-a=0 y no de la forma x=a.

Con el comando «algsys» resolvemos el sistema de ecuaciones, y obtenemos la siguiente solución:

$\begin{matrix} a_{1}=1 \\b_{1}=0 \\ c_{1}=0\\d_{1}=\frac{1}{8} \\a_{2}=2 \\b_{2}=\frac{3}{2} \\ c_{2}=\frac{3}{4}\\d_{2}=-\frac{1}{4} \end{matrix}$

Por tanto, podemos construir las dos splines:

$S_{1}(x)=1+\frac{1}{8}(x-1)^{3} , x\in [1,3]$

$S_{2}(x)=2+\frac{3}{2}(x-2)+\frac{3}{4}(x-2)^{2}-\frac{1}{4}(x-2)^{3}, x\in [3,4]$

Y ahora hacemos la comprobación con Maxima. Esas splines evaluadas en los nodos tienen que dar sus imágenes correspondientes:

S1solucion: 1+(1/8)*(x-x_[1])^3; S2solucion: 2+(3/2)*(x-x_[2])+(3/4)*(x-x_[2])^2-(1/4)*(x-x_[2])^3; Comprobacionnodo1: ev(S1solucion,x=x_[1]); Comprobacionnodo2: ev(S1solucion,x=x_[2]); Comprobacionnodo2_: ev(S2solucion,x=x_[2]); Comprobacionnodo3: ev(S2solucion,x=x_[3]);

Como vemos, los resultados coinciden, lo que indica que hemos hecho bien la programación y ya tenemos las 2 splines cúbicas.

Podemos dibujar las splines y estimar el valor para el cual queríamos hacer la interpolación, es decir, ¿cuál sería el valor de satisfacción del cliente con 2 empleados en el establecimiento?.

Para ello empleamos la primea spline que es la que pasa por los dos nodos que contienen al valor en cuestión, y su resultado es 1.125. Con Maxima lo podemos hacer fácilmente, y además representarlo en un gráfico:

x_:[1,3,4,6,7,8,9,10,11,12]; fx:[1,2,4,5,7,9,2,10,10,10]; x_interpolar:2; f_S1solucion: ev(S1solucion,x=x_interpolar), numer; plot2d([[discrete, x_, fx], [discrete, [[x_interpolar,f_S1solucion]]],S1solucion,S2solucion], [x,0,15],[y,0,10], [style, points, points, lines,lines], [color,green, red, orange,magenta], [xlabel, «Número de empleados»], [ylabel, «Satisfacción del cliente»], [legend, false]);

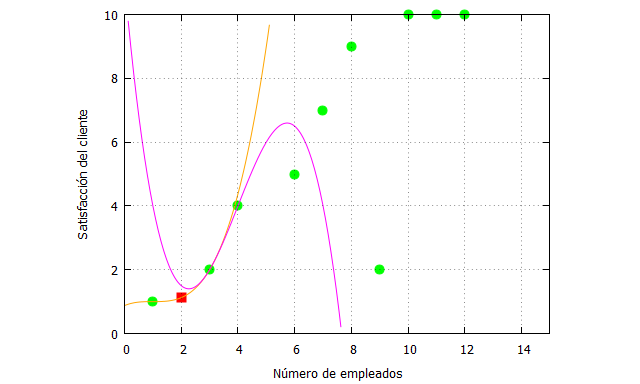
La curva naranja representa la primera spline y la curva rosa la segunda. Podemos hacer una comprobación con el comando de Maxima «cspline» y veremos que nos da el mismo resultado:

S1solucion: 1+(1/8)*(x-x_[1])^3, expand; S2solucion: 2+(3/2)*(x-x_[2])+(3/4)*(x-x_[2])^2-(1/4)*(x-x_[2])^3,expand; load (interpol); p:[[1,1],[3,2],[4,4]]; cspline(p);

Conclusión

Las splines cúbicas son una muy interesante forma de realizar interpolaciones, probablemente una de las que más ventajas conlleva y que permite realizar aproximaciones más fiables. Su procedimiento en Maxima es un poco laborioso, pero si seguimos ordenadamente los pasos que surgen de las restricciones del método, no debemos tener problema.

Category: METODOLOGÍA DE INVESTIGACIÓN