Continuamos con una introducción sencilla al análisis de datos. Tras comparar los resultados de las splines cúbicas y el método de mínimos cuadrados, debemos ahora plantearnos algunas cuestiones sobre la idoneidad de lo que hemos hecho hasta ahora, y las opciones que aparecen entonces. Lo vamos a hacer de forma muy simple, para estimular el interés de los estudiantes hacia cuestiones más complejas.
Datos de partida
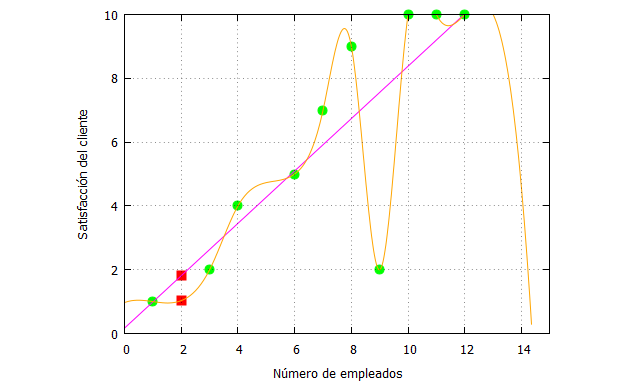
Recordemos que tenemos los siguientes datos analizados con splines y mínimos cuadrados:
| load (interpol); p:[[1,1],[3,2],[4,4], [6,5],[7,7],[8,9],[9,2],[10,10],[11,10],[12,10]]; splines: cspline(p); x_:[1,3,4,6,7,8,9,10,11,12]; fx:[1,2,4,5,7,9,2,10,10,10]; x_aproximar:2; x_interpolar:x_aproximar; fx_estimada:0.8212147134302823*z+0.1693755346449957; fx_estimada_x_aproximar: ev(fx_estimada, z=x_aproximar), numer; f_splines: ev(splines,x=x_interpolar), numer; plot2d([[discrete, x_, fx], [discrete, [[x_aproximar,fx_estimada_x_aproximar], [x_interpolar,f_splines]]],fx_estimada,splines], [x,0,15],[y,0,10], [style, points, points, lines, lines], [color, green, red, magenta, orange, magenta], [xlabel, “Número de empleados”], [ylabel, “Satisfacción del cliente”], [legend, false]); |
Capacidad explicativa
La capacidad explicativa del modelo ajustado por mínimos cuadrados se suele medir con el coeficiente de determinación (R-cuadrado), que es una medida de la varianza explicada por el modelo, es decir, cuantifica la importancia de la varianza de error, y que está entre 0 y 1 (siendo 1 el ajuste perfecto). Se obtiene por el cociente entre la varianza de los datos ajustados frente a la de las imágenes de los datos observados.
En Maxima podemos obtenerlo así:
| load(descriptive); varianza_fx:var1(fx_traspuesta), numer; ajuste: transpose(ev(fx_estimada,z=x)); varianza_fx_estimada:var1(ajuste); R_cuadrado:(varianza_fx_estimada/varianza_fx); |
El resultado es:
Pero debemos plantearnos dos cuestiones fundamentales tras inspeccionar gráficamente los datos. En primer lugar, la hipótesis de relación lineal parece no cumplirse a medida que el número de empleados crece. Y en segundo lugar el dato [9,2] puede ser un dato atípico, un outlier que por diferentes razones (sean aleatorias o no), nos está condicionando la estimación, y que quizá habría que estudiar obviar.
Parte lineal ¿Cómo sería el ajuste si sólo nos centramos en el rango de datos [1,8]? Vamos a verlo:
| x:matrix([1,3,4,6,7,8]); fx:matrix([1,2,4,5,7,9]); x_traspuesta: transpose(x); fx_traspuesta:transpose(fx); n: length(x_traspuesta); datos: zeromatrix(n,1); datos_xcuad:x_traspuesta.x; datos_y:fx_traspuesta; datos_xy:fx_traspuesta.x; datos_x: x_traspuesta; print(datos_xcuad,datos_y, datos_xy,datos_x); suma_xcuad:sum(datos_xcuad[i,i],i,1,n); suma_y:sum(datos_y[i,1],i,1,n); suma_xy:sum(datos_xy[i,i],i,1,n); suma_x:sum(datos_x[i,1],i,1,n); cuad_suma_x:suma_x^2; alpha:((suma_xcuad*suma_y)-(suma_xy*suma_x))/((n*suma_xcuad)-cuad_suma_x), numer; beta:((n*suma_xy)-(suma_x*suma_y))/((n*suma_xcuad)-cuad_suma_x), numer; fx_estimada:alpha+beta*z; |
Lo que nos da la siguiente recta de ajuste (la estimación de la función). 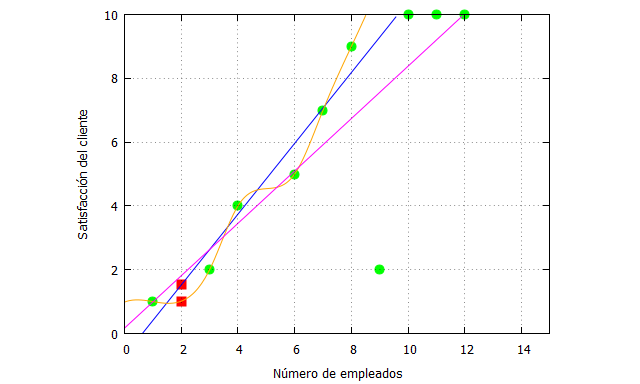
Entonces podemos hacer la representación gráfica del ajuste de los datos: La recta azul es la nueva función de ajuste, cuya capacidad explicativa es:
El ajuste es mucho mejor, claramente. Lo que sucede es que sólo podemos hacer esta acción si podemos justificar muy bien esa estimación de mínimos cuadrados para sólo una parte de los datos empíricos.
Los outliers pueden surgir aleatoriamente, y es parte de la variabilidad global, pero en detemrinados casos podemos intentar eliminarlos si sospechamos que hay “algo raro” en ese dato (alguna variación sistemática que ha producido un valor extraño).
Viendo gráficamente los datos, y teniendo en cuenta el contexto teórico, está claro de que hay un punto de saturación donde por más que se añadan vendedores no se incrementa el nivel de satisfacción (es máximo ya con 10 vendedores). Por tanto, no tiene mucho sentido intentar modelar esa parte de los datos junto al resto.
Conclusión
Hemos visto que, a veces, y si la teoría y la perspicacia del investigador lo permiten, podemos descartar algunos datos para obtener ajustes mucho mejores, y de este modo, realizar predicciones más fiables en el rango de datos que nos interese. No siempre, desde luego, ello es recomendable, pero la idea es que a los datos hay que mirarlos muy bien antes de analizarlos.
Hay dos aspectos fundamentabes que no hemos tocado aquí, pero que son inherentes a cualquier éxito en los análisis: (1) El modelo teórico tiene que estar causalmente bien especificado, no importa la R-cuadrado (aunque sea alto) si no es teóricamente plausible esa relación; (2) El planteamiento de un modelo estadístico es también el de sus asunciones, las cuales no hemos testado en su totalidad, como por ejemplo, si la varianza de error es homogénea.
En futuros posts iremos aclarando mejor estas y otras cuestiones.
