Expondremos aquí la segunda parte del segundo capítulo de: Probability Theory and Statistical Inference, de Aris Spanos. Tras explicar la estructura básica de un modelo estadístico simple, continuamos avanzando en el desarrollo de conceptos fundamentales.
Muestra aleatoria
Una muestra aleatoria asume dos características fundamentales: independencia e idéntica distribución.
Las variables aleatorias son independientes si la probabilidad de ocurrencia de cualquiera de ellas no influye y no ha sido influida por la ocurrencia de cualquier otra del conjunto.
La idéntica distribución se da cuando sus funciones de densidad son iguales, es decir:
Spanos va muy despacio introduciendo todos estos conceptos, que posteriormente serán desarrollados con más detalle. Por eso, nosotros vamos a ir también de la mano del autor, comentando ejemplos sencillos.
Cojamos de nuevo a Kemba Walker y sus puntos por minutos en los 82 partidos jugados en 2018/19, y vamos a generar 4 muestras aleatorias de 60 observaciones cada una. Para ello hemos empleado el generador de números aleatorios de XLStat, que se puede integrar en Excel. Una vez que se han generado las 4 muestras, las llevamos a Maxima para su gestión gráfica:
kill (all);
data:read_matrix(file_search("RUTADELARCHIVO.txt"));
datatranspose:transpose(data);
walker1:datatranspose[1];
histogram (
walker1,
nclasses=11,
frequency=density,
xlabel="Espacio muestral",
ylabel="Densidad de probabilidad",
fill_color=green,
fill_density=0.5);
kill (all);
data:read_matrix(file_search("RUTADELARCHIVO.txt"));
datatranspose:transpose(data);
walker2:datatranspose[2];
histogram (
walker2,
nclasses=11,
frequency=density,
xlabel="Espacio muestral",
ylabel="Densidad de probabilidad",
fill_color=green,
fill_density=0.5);
kill (all);
data:read_matrix(file_search("RUTADELARCHIVO.txt"));
datatranspose:transpose(data);
walker3:datatranspose[3];
histogram (
walker3,
nclasses=11,
frequency=density,
xlabel="Espacio muestral",
ylabel="Densidad de probabilidad",
fill_color=green,
fill_density=0.5);
kill (all);
data:read_matrix(file_search("RUTADELARCHIVO.txt "));
datatranspose:transpose(data);
walker4:datatranspose[4];
histogram (
walker4,
nclasses=11,
frequency=density,
xlabel="Espacio muestral",
ylabel="Densidad de probabilidad",
fill_color=green,
fill_density=0.5);
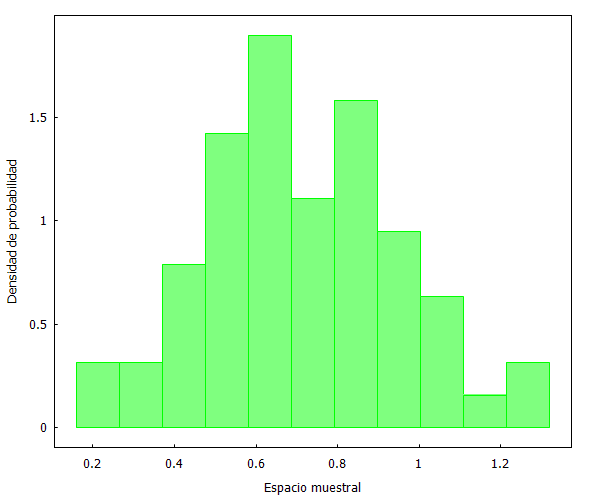
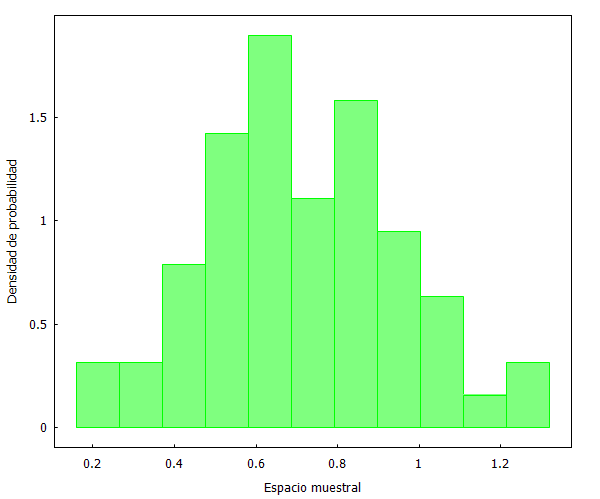
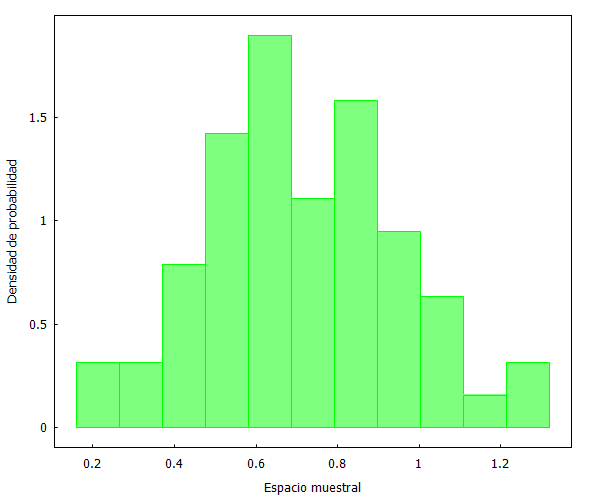
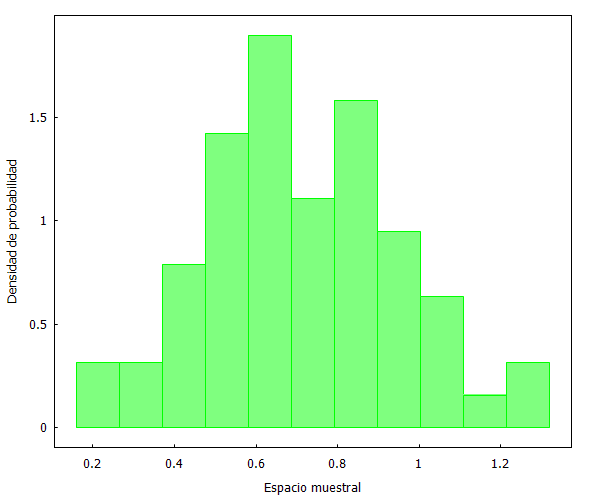
Como se puede apreciar, las distribuciones son prácticamente idénticas. Pero, ¿qué sucedería ahora si escogemos una muestra no aleatoria? Lo comprobamos a continuación seleccionando los primeros y últimos 60 partidos.
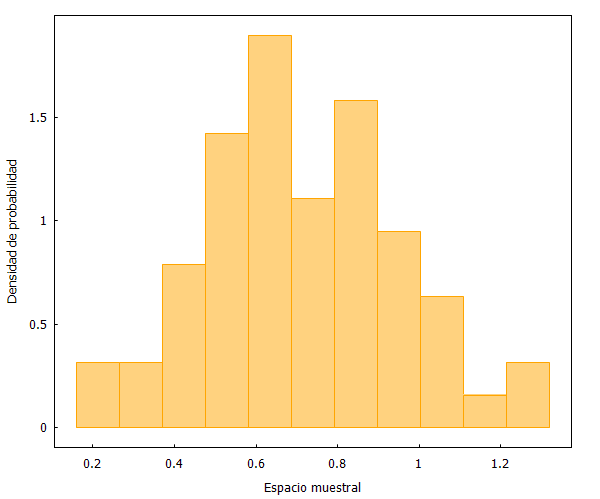
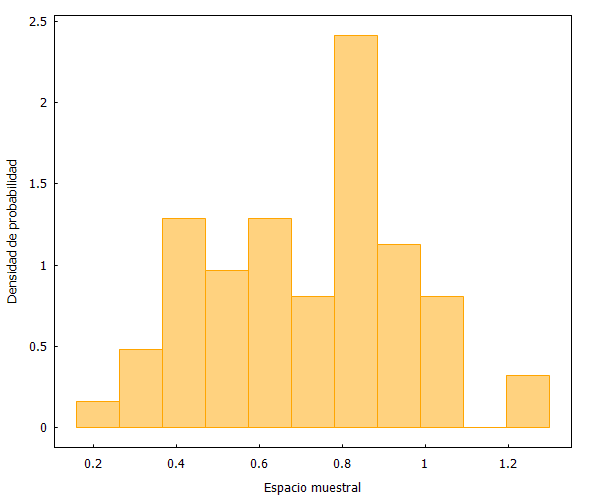
Y aquí podemos ver dos fenómenos curiosos. En primer lugar, que la selección no aleatoria de los primero 60 partidos se distribuye de forma similar a las muestras aleatorias anteriores. Y en segundo lugar, que la selección no aleatoria de los últimos 60 partidos refleja un cambio ostensible en la forma de la distribución de datos.
Las consecuencias que tienen las dos últimas figuras las iremos comentando más adelante. Pero ya advertimos un corolario preliminar: Una muestra no aleatoria puede distribuirse igual que una aleatoria o no.
Sin embargo, además, hemos de ser conscientes de que muestras aleatorias de tamaños diferentes pueden diferir en su apariencia. Por ejemplo, si ahora seleccionamos 2 muestras aleatorias de 30 observaciones, obtenemos lo siguiente:
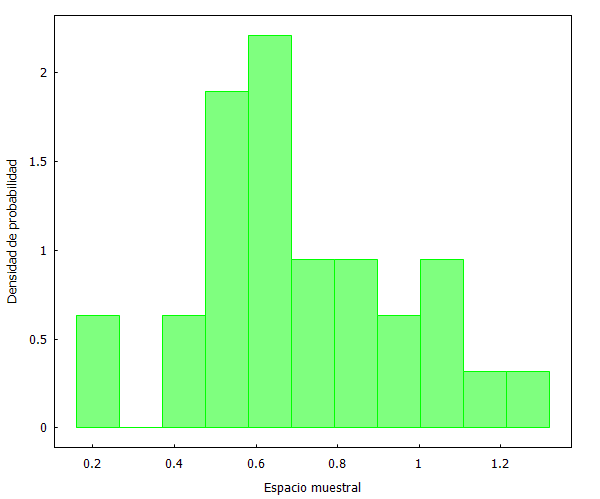
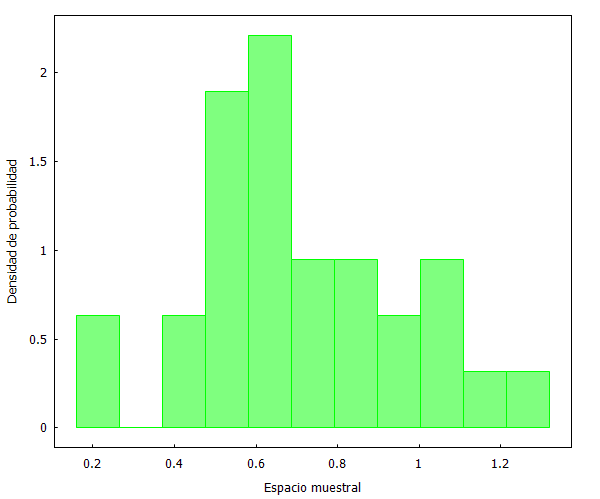
Esa apariencia es diferente de la mostrada cuando se escogían 60 observaciones.
Hay que tener en cuenta de que estamos hablando de distribuciones muestrales, y que en la definición de Spanos no se pretende ir más allá de los conceptos de independencia e idéntica distribución de las variables aleatorias.
Y es aquí donde quizá aparezca la confusión, porque Spanos en la página 33 habla sobre una única variable aleatoria X, mientras que en la página 38 especifica un conjunto de variables aleatorias. En realidad, en el ejemplo del rendimiento del jugador de baloncesto, los puntos por minuto es una única variable aleatoria que se distribuye de una determinada forma. Una muestra aleatoria de esa varibale requiere que todas las observaciones tengan la misma probabilidad de ser seleccionadas. Las diferentes muestras aleatorias que se puedan recoger deberán ser también independientes, y esas muestras serán a su vez variables aleatorias que idealmente se distribuirán de forma equivalente.
Sí, quizá estamos adelantando conceptos, pero es necesario hacerlo para manejarnos en esta complejidad técnica.
Seguiremos con la tercera parte de este segundo capítulo en posteriores posts.
