Continuamos con el segundo capítulo de: Probability Theory and Statistical Inference, de Aris Spanos. Debido a su extensión, lo dividiremos en partes, en aras de hacer más sencillo el estudio paso a paso.
Capítulo II. Teoría de la probabilidad: Un marco para modelar
La teoría de la probabilidad provee la base fundacional y el marco de referencia para la modelización de datos y la inferencia estadística.
La inferencia estadística es eminentemente inductiva, ya que establece conclusiones de los observables más allá de estos. De este modo, los datos observados son vistos como una realización particular de un mecanismo estocástico que se ha especificado por el modelo estadístico postulado a priori.
Estructura básica de un modelo estadístico simple
Un modelo estadístico tiene 2 componentes:
(1) Modelo de probabilidad:
(2) Modelo de muestreo: es una muestra aleatoria
Lo que nos dicen estas dos componentes es que el modelo de probabilidad especifica una familia de densidades definida sobre el rango de valores de la variable aleatoria
; una función de densidad para cada valor del parámetro
, que tiene un rango de valores determinado por
.
Chebyshev definió de forma simple una variable aleatoria como una variable real que puede asumir diferentes valores con diferentes probabilidades.
Una variable aleatoria es una función de un conjunto de resultados a la recta real, asignando números a esos resultados. Por ejemplo, con 2 dados:
Por tanto, lo que tenemos aquí es una función que relaciona a un conjunto posible de resultados con números de la recta real. En el primer caso, esos números coinciden con la suma de los números posibles al lanzar los dados, y en el segundo, hacer referencia a cuando el resultado es par o impar. En ambos casos, tenemos variables aleatorias. Es obvio deducir que , es la recta real. Y también es sencillo estipular que
Cualquiera que sea la variable aleatoria tiene que cumplir lo siguiente:
Es decir, que la probabilidad de un resultado particular siempre es cero o positiva, y que la suma de todas las probabilidades del conjunto de resultados de la recta real es 1.
Cuando esos números de la recta real son un conjunto infinito, la distribución es continua en lugar de discreta, y entonces:
¿Cómo definiriamos una variable aleatoria X que represente el lanzamiento de un tiro libre en baloncesto? Podría ser de la siguiente forma:
Aquí vemos que el conjunto de resultados posible es , que representan un fallo y un acierto, respectivamente. Ese conjunto se «traslada» a la recta real en forma de dos números, 0 y 1, que representan también el fallo y el acierto. Y a cada uno de esos números se le asigna una probabilidad.
Por ejemplo, el jugador de los Mavs, Luka Doncic, ha tenido un 71.3% de acierto en los tiros libres en la temporada 2018/19. Podríamos entonces estipular que:
En Maxima lo podríamos representar así:
f_0:0.287; f_1: 0.713; plot2d([discrete,[[0,f_0],[1,f_1]]], [x,0,1],[y,0,1], [style, points, points],[color, red, green], [xlabel, "Resultado: fallo (0), acierto (1)"], [ylabel, "Función de densidad"], [legend, false]);
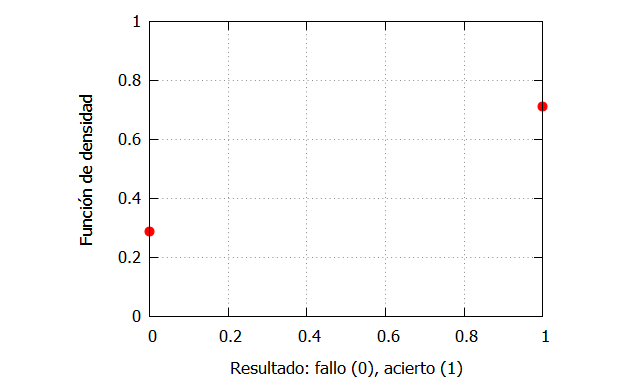
La función de densidad que podríamos definir para el caso anterior sería:
que es la función de densidad de Bernouilli.
Fijémonos en lo que hemos hecho: hemos construido una función de densidad que nos dice en cada momento, es decir, para cada valor de x, la probabilidad de ese valor. Ese valor de probabilidad está en función de un parámetro desconocido, cuyo rango de valores coincide con el rango de valores de probabilidad, pero no siempre tiene que ser así, como veremos más adelante.
Como bien indica Spanos, la repetición de n ensayos de Bernouilli nos da la distribución binomial cuya función de densidad es:
donde:
Así, podríamos calcular, por ejemplo, la probabilidad de que Luka Doncic anotara los 3 tiros libres que lanza cuando le hacen una falta personal en un triple:
Pero aquí ya hemos cambiado el escenario, ya no tenemos la misma variable aleatoria que antes, sino la siguiente:
El conjunto de resultados es 8 porque son las variaciones con repetición de 2 elementos tomados de 3 en tres.
Por tanto:
Es decir, la probabilidad de que Luka Doncic anote los 3 lanzamientos libres es del 36.2%.
Obviamente, todos estos análisis los hemos realizado suponiendo independencia en los tiros libres, algo que la investigación en baloncesto nos dice que es cuestionable.
Podemos escribir una función en Maxima para representar esos valores de la distribución binomial, que recordemos que es discreta, pero hemos añadido una curva para que se aprecie la tendencia.
kill (all); tiroslibres(n,x,fi):=binomial(n,x)*fi^x*(1-fi)^(n-x); funcion(x):=tiroslibres(3,x,0.713); ceroaciertos:funcion(0); unacierto:funcion(1); dosaciertos:funcion(2); tresaciertos:funcion(3); plot2d([funcion(x),[discrete,[[0,ceroaciertos], [1,unacierto],[2,dosaciertos], [3,tresaciertos]]]], [x,0,3],[y,0,1], [style, lines, points],[color, green, red], [xlabel, "Resultado (aciertos)"],[ylabel, "Función de densidad"], [legend, false]);
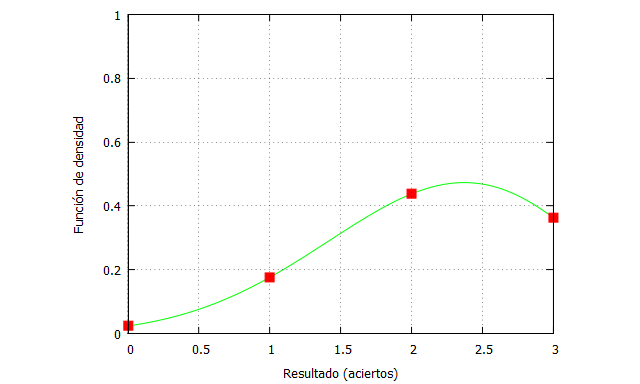
Como se puede ver, lo más probable es que Doncic anote 2 de los 3 tiros libres. Si incrementamos el número de ensayos, la distribución se aproxima a una Normal, algo que también veremos más adelante, donde el máximo de probabilidad coincide con el valor del parámetro .
kill (all); tiroslibres(n,x,fi):=binomial(n,x)*fi^x*(1-fi)^(n-x); funcion(x):=tiroslibres(100,x,0.713); setentayunaciertos:funcion(71); plot2d([funcion(x),[discrete,[ [71,setentayunaciertos]]]], [x,0,100],[y,0,0.1], [style, lines, points],[color, green, red], [xlabel, "Resultado (aciertos)"],[ylabel, "Función de densidad"], [legend, false]);
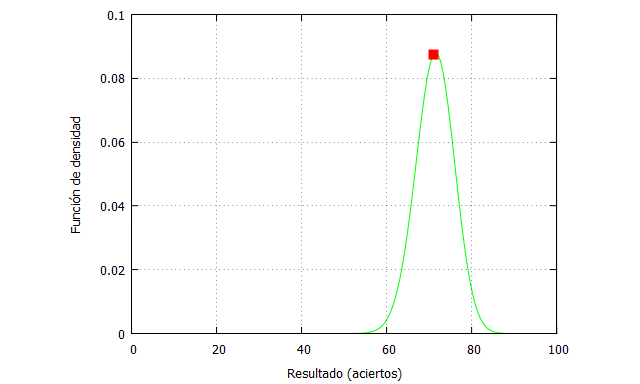
Podemos ahora comparar esas curvas de probabilidad entre diferentes jugadores, que tienen habilidades dispares. El porcentaje de Doncic es discreto para un jugador de ese nivel, el de Anthony Davis es bueno (79.4%) y el de James Harden es muy bueno (87.9%).
A la hora de encarar una serie de 3 tiros libres:
kill (all); tiroslibres(n,x,fi):=binomial(n,x)*fi^x*(1-fi)^(n-x); n:3; Doncic(x):=tiroslibres(n,x,0.713); Davis(x):=tiroslibres(n,x,0.794); Harden(x):=tiroslibres(n,x,0.879); plot2d([Doncic(x),Davis(x),Harden(x)], [x,0,n],[y,0,1], [style, lines,lines, lines],[color, green, blue, orange], [xlabel, "Resultado (aciertos)"],[ylabel, "Función de densidad"], [legend, "Doncic", "Davis", "Harden"]);
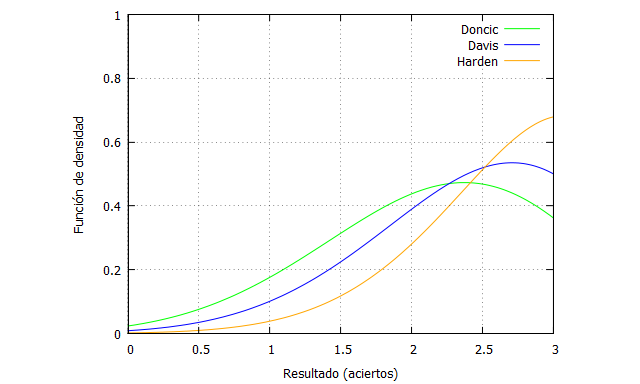
Tanto Davis como Harden tienen más probabilidad de encestar los 3 que de encestar 2, no así, como hemos dicho, Doncic.
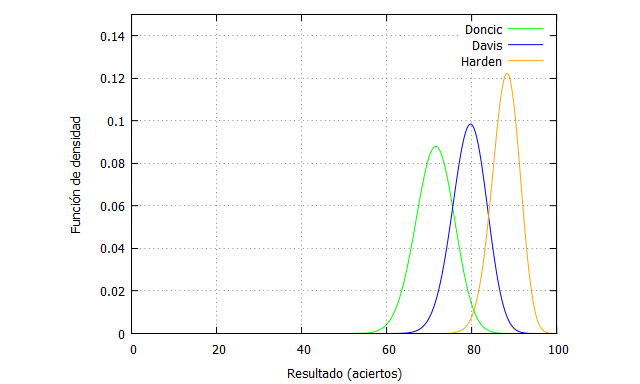
Y si miramos ahora a una serie de 100 tiros libres, se puede apreciar mejor las curvas de probabilidad, que reflejan la habilidad de estos jugadores.
kill (all); tiroslibres(n,x,fi):=binomial(n,x)fi^x(1-fi)^(n-x); n:100; Doncic(x):=tiroslibres(n,x,0.713); Davis(x):=tiroslibres(n,x,0.794); Harden(x):=tiroslibres(n,x,0.879); plot2d([Doncic(x),Davis(x),Harden(x)], [x,0,n],[y,0,0.15], [style, lines,lines, lines],[color, green, blue, orange], [xlabel, "Resultado (aciertos)"],[ylabel, "Función de densidad"], [legend, "Doncic", "Davis", "Harden"]);
Continuaremos con la segunda parte de este capítulo II en próximos posts.

3 comentarios en «TEORÍA DE PROBABILIDAD E INFERENCIA ESTADÍSTICA SEGÚN ARIS SPANOS (IIa)»
Los comentarios están cerrados.