Una vez introducidos en los campos direccionales y en la filosofía de análisis de las ecuaciones diferenciales, vamos a complicar un poco más el caso a estudiar. Ahora, tenemos que el crecimiento de la población de individuos, es decir, la derivada de la población con respecto al tiempo no sólo depende de la propia población (y del tiempo, claro), sino que lo hace también de otra población que actúa como limitante.
Pensemos en una población de presas (conejos) y una de predadores (zorros). A la primera la llamaremos x, y a la segunda y. En este post vamos a mostrar qué sucede cuando existe esa dependencia, mostrando la propuesta de Lotka-Volterra.
Ecuaciones de Lotka-Volterra
Comenzamos especificando la ecuación:
Ahora tenemos dos parámetros más, alfa y beta. El primero representa la tasa de natalidad de las presas (conejos), y el segundo la de mortalidad cuando se encuentran con los predadores (zorros). Por tanto, el crecimiento dependerá de la diferencia entre los que nazcan y los que mueran.
Del mismo modo, podemos pensar que la población de zorros depende de la de conejos, si no hay otras presas que cazar. La ecuación de crecimiento para los zorros sería:
Aquí representa una especie de tasa de transferencia energética en cada interacción entre zorros y conejos, y
la tasa de mortalidad de los zorros.
Se crea, por tanto, una interdependencia entre ambas poblaciones, siendo complejo a nivel intuitivo predecir cómo evolucionarán en el tiempo.
Solución de la ecuación
Podemos dividir ambas ecuaciones, y llegar a esta expresión:
De este modo, podemos intentar resolverla con Maxima. Para ello, hemos de especificar un valor para los 4 parámetros, y también unas condiciones iniciales para las dos variables: conejos y zorros.
En cuanto al valor de los parámetros, especificamos lo siguiente:
Y también exploramos dos condiciones iniciales. En la primera (y=6 , x=2), y en la segunda (y=2 , x=2). Podemos ya, entonces, programar el siguiente código:
| A:0.5;B:0.5;C:0.5;D:0.5; ecuacionLotkaVolterra: ‘diff(y,x) -(((C*x*y)-(D*y))/((A*x)-(B*x*y)))=0; solucionLotkaVolterra: ode2(ecuacionLotkaVolterra,y,x); solucionfinal_1: ic1(solucionLotkaVolterra,y=6,x=2); solucionfinal_2: ic1(solucionLotkaVolterra,y=2,x=2); load(implicit_plot); implicit_plot([solucionfinal_1,solucionfinal_2] ,[y,0,8],[x,0,8], [ylabel, «Zorros»], [xlabel, «Conejos»], [legend, false]); |
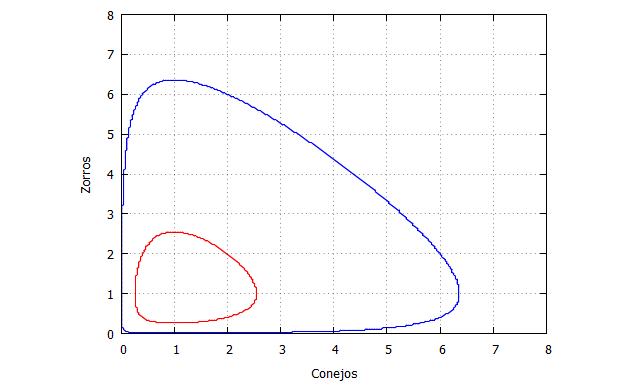Hay que observar que, aunque el tiempo se incremente indefinidamente la dinámica del sistema está regida por el conjunto límite que representa cada una de las curvas solución. Las poblaciones crecen y decrecen siempre de la misma forma.
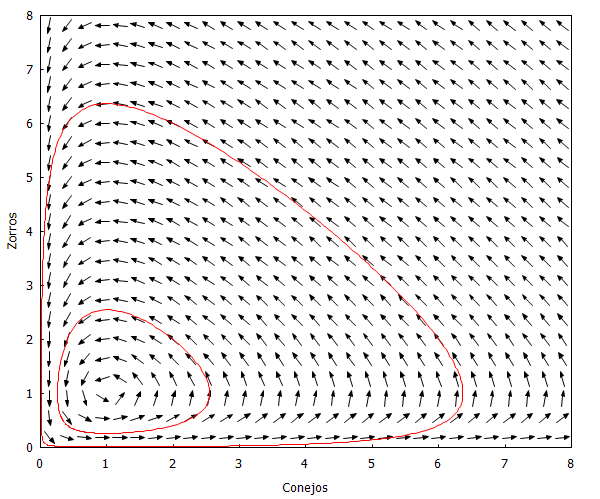
Podemos representar los campos direccionales también:
| load(drawdf)$ drawdf([x*(0.5-0.5*y),-y*(0.5-0.5*x)],[x,0,8], [y,0,8],[xlabel=»Conejos»], [ylabel=»Zorros»],[trajectory_at,2,6],[trajectory_at,2,2]); |
Conejos y zorros en el tiempo
Nos falta ahora conocer la evolución de los conejos y zorros en el tiempo. En realidad ya hemos visto que deber ser un recorrido periódico, aunque nos queda la duda de qué sucede realmente en el caso en que y=6 y x=2, porque parece que hay un momento en el que la trayectoria indica que la población de conejos y zorros es cero.
Para representar esa evolución temporal de las poblaciones, hemos de emplear el método de Runge-Kutta para obtener una solución numérica. Vamos a ayudarnos del material creado por el profesor Renato Álvarez.
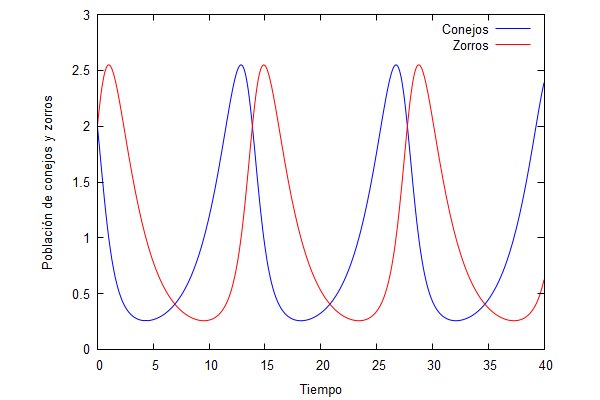
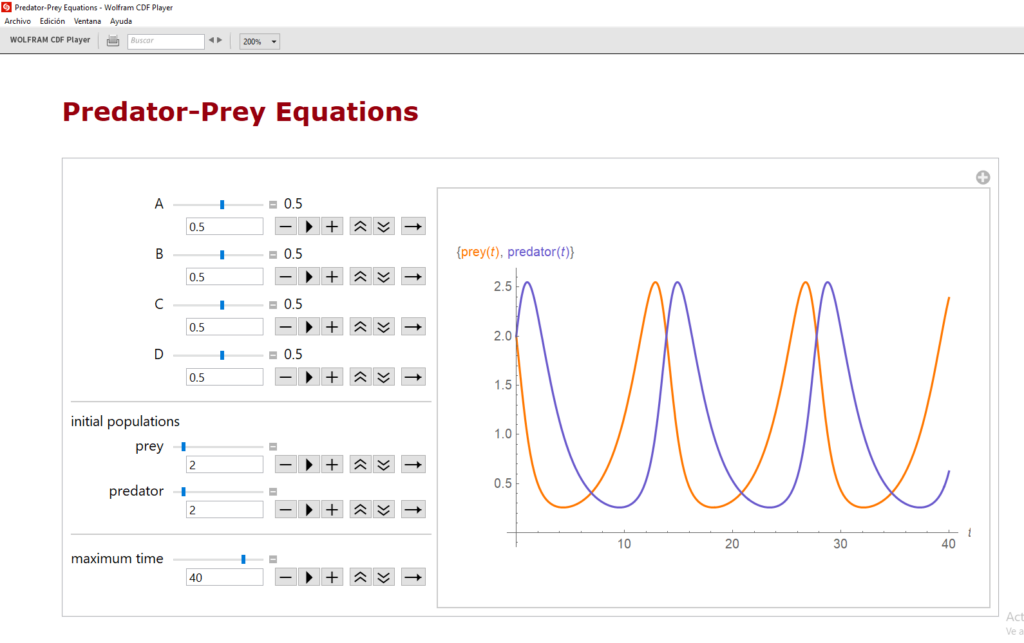
Para el caso de 2 conejos y 2 zorros (x=2, y=2), obtenemos lo siguiente:
| kill (all);
sol:rk([x*(0.5-0.5*y),-y*(0.5-0.5*x)],[x,y],[2,2],[t,0,40,0.1]); x:makelist([sol[k][1],sol[k][2]],k,1,length(sol))$ wxplot2d([[discrete,x],[discrete,y]],[legend, «Conejos», «Zorros»], |
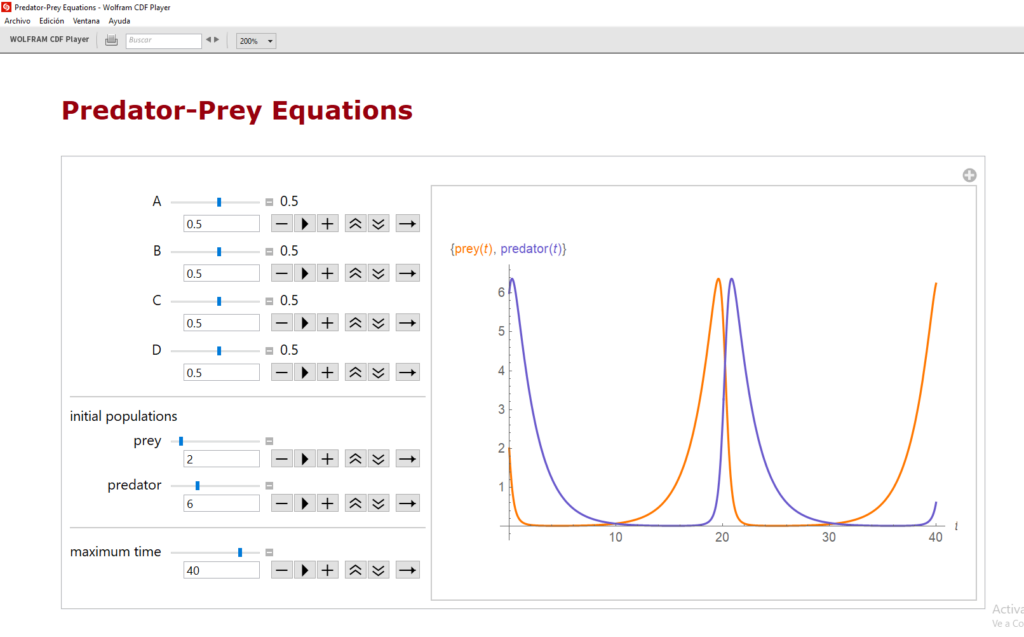
Pero para el caso de 2 conejos y 6 zorros (x=2, y=6), obtenemos lo siguiente:
| kill (all);
sol:rk([x*(0.5-0.5*y),-y*(0.5-0.5*x)],[x,y],[2,6],[t,0,40,0.1]); x:makelist([sol[k][1],sol[k][2]],k,1,length(sol))$ wxplot2d([[discrete,x],[discrete,y]],[legend, «Conejos», «Zorros»], |
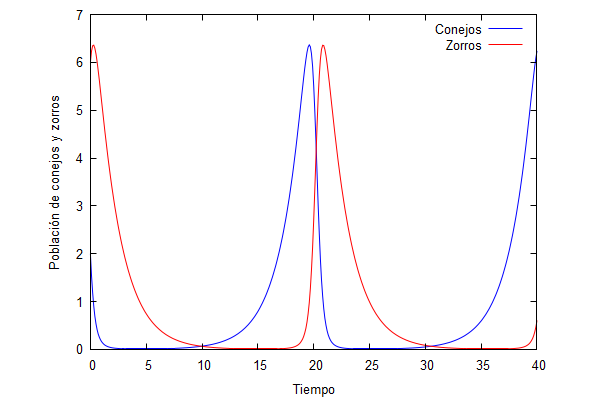
Por tanto, los conejos se extinguen en esta segunda situación y, si no hay un repoblamiento o entran nuevos conejos en el hábitat, la población de zorros también se extinguirá.
Un recomendable texto para introducirse en el significado de la interdependencia puede encontrarse aquí. Al mismo tiempo, los estudiantes pueden explorar de manera interactiva el comportamiento del sistema acoplado en las demostraciones de Wolfram.
Como puede verse en estos dos «pantallazos», los resultados concuerdan con nuestra programación (los colores están cambiados)
Conclusión
En esta simple introducción a la dinámica de la interacción para ilustrar la complejidad, los alumnos de marketing pueden comprobar que, cuando existe acoplamiento, el comportamiento de las poblaciones es extremadamente difícil de inferir sin ayuda de las matemáticas.
Los parámetros pueden variar (aquí los hemos mantenido todos igual a 0.5), y las condiciones iniciales también. Es más, el modelo se puede complicar con la introducción de competencia en el hábitat (los conejos compiten por recursos limitados de alimentación) y otras restricciones en las ecuaciones.
Todo esto nos sirve para entender que cuando se planea una intervención sobre un sistema acoplado que está en homeóstasis, las consecuencias sobre el sistema pueden ser contra intuitivas o indeseables Y aquí el alumno puede imaginar sistemas biológicos, económicos, políticos, etc.