AJUSTE DE FUNCIONES (I): SPLINES VS MÍNIMOS CUADRADOS

Tras explicar varios de los más empleados métodos de interpolación para buscar aproximarnos a la función que describe los datos empíricos, hemos visto que las splines cúbicas nos ofrecen mucha flexibilidad. Sin embargo, y aunque pueda parecer paradójico, el hecho de buscar una función de interpolación que pase por todos los nodos puede ser contraproducente, porque podemos estar dando demasiada importancia al ruido, cuando lo que buscamos es la señal. Es decir, cuando en los datos hay errores aleatorios (y también algún error sistemático puntual), buscar aproximaciones con funciones que no pasen necesariamente por esos nodos pero que tengan otras propiedades (como la minimización de una variable de error), puede ser más útil.

El método básico para realizar este ajuste es el de mínimos cuadrados, un potente método no paramétrico que minimiza la suma al cuadrado de los errores. Y es lo que vamos a ver en este post, aunque da manera muy simplificada ya que está sobradamente explicado en multitud de textos especializados de prácticamente todas las áreas científicas.

Así, compararemos gráficamente el ajuste por mínimos cuadrados con el método de las splines cúbicas, para estimular la reflexión de los alumnos.

Datos de partida

Usaremos los mismos datos que en el método de Lagrange, y en el de todos los ejemplos sobre interpolación:

x	f(x)
1	1
3	2
4	4
6	5
7	7
8	9
9	2
10	10
11	10
12	10

Estos datos relacionan la cantidad de empleados utilizados en un gran supermercado (x) con la saltisfacción del cliente $y=f(x)$ . La satisfacción del cliente se mide en una escala de 0 a 10, donde 0 es el valor mínimo y 10 el valor máximo.

x_:[1,3,4,6,7,8,9,10,11,12]; fx_:[1,2,4,5,7,9,2,10,10,10]; plot2d([discrete, x_, fx_], [x,0,15],[y,0,10], [style, points], [color,green], [xlabel, «Número de empleados»], [ylabel, «Satisfacción del cliente»], [legend, false]);

Splines cúbicos

Una vez que ya sabemos programar las splines paso a paso, podemos actuar de forma más directa con Maxima, pidiendo que use todos los datos disponibles:

load (interpol); p:[[1,1],[3,2],[4,4], [6,5],[7,7],[8,9],[9,2],[10,10],[11,10],[12,10]]; splines: cspline(p);

Y lo podemos graficar de la siguiente forma:

x_:[1,3,4,6,7,8,9,10,11,12]; fx:[1,2,4,5,7,9,2,10,10,10]; plot2d([[discrete, x_, fx], splines], [x,0,15],[y,0,10], [style, points, lines], [color,green, orange], [xlabel, «Número de empleados»], [ylabel, «Satisfacción del cliente»], [legend, false]);

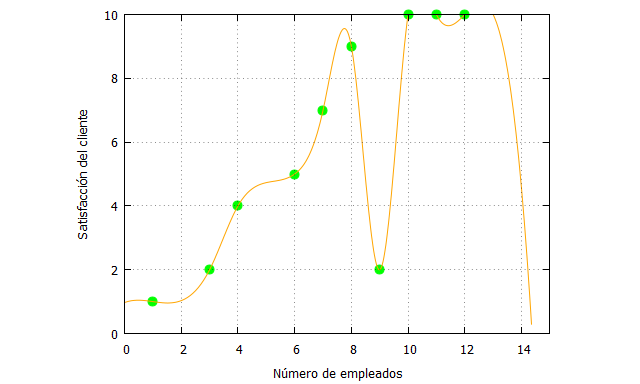
Vemos que las splines hacen aparentemente un «buen trabajo» de ajuste, pero tenemos ese punto «problemático» [9,2] que hace que la curva de interpolación cambie drásticamente. Sin embargo, en este caso no nos afecta demasiado a nuestro objetivo de interpolar puntos que no están en los datos en el intervalo [1,12]. Tanto el nodo 2 como el nodo 5 se pueden evaluar con la curva de interpolación ya que las splines van de nodo a nodo, por lo que ese comportamiento «raro» en el punto [9,2] no afecta prácticamente a las evaluaciones entre los otros nodos.

Mínimos cuadrados lineales

Este método se basa en la minimización de la función de error:

$E(\alpha,\beta)=\sum_{i=1}^{n}(f(x_{i})-(\beta}x_{i}+\alpha))^{2}$

donde $y_{i}=f(x_{i})$ se corresponde con las imágenes de los datos brutos $x_{i}$ , y $\alpha,\beta$ son parámetros a estimar.

Minimizar esa función requiere que:

$\frac{\partial E }{\partial \alpha}=0$

$\frac{\partial E }{\partial \beta}=0$

Es importante señalar que se asume que el error tiene de media cero, es decir, es aleatorio (ruido blanco).

De este modo:

$\alpha=\frac{\sum_{i=1}^{n}x_{i}^{2}\sum_{i=1}^{n}y_{i}-\sum_{i=1}^{n}y_{i}x_{i}\sum_{i=1}^{n}x_{i}}{n\sum_{i=1}^{n}x_{i}^{2}-(\sum_{i=1}^{n}x_{i})^{2}}$

$\beta=\frac{n\sum_{i=1}^{n}x_{i}y_{i}-\sum_{i=1}^{n}x_{i}\sum_{i=1}^{n}y_{i}}{n\sum_{i=1}^{n}x_{i}^{2}-(\sum_{i=1}^{n}x_{i})^{2}}$

Así, podemos programarlo con Maxima usando el siguiente código:

x:matrix([1,3,4,6,7,8,9,10,11,12]); fx:matrix([1,2,4,5,7,9,2,10,10,10]); x_traspuesta: transpose(x); fx_traspuesta:transpose(fx); n: length(x_traspuesta); datos: zeromatrix(n,1); datos_xcuad:x_traspuesta.x; datos_y:fx_traspuesta; datos_xy:fx_traspuesta.x; datos_x: x_traspuesta; print(datos_xcuad,datos_y, datos_xy,datos_x); suma_xcuad:sum(datos_xcuad[i,i],i,1,n); suma_y:sum(datos_y[i,1],i,1,n); suma_xy:sum(datos_xy[i,i],i,1,n); suma_x:sum(datos_x[i,1],i,1,n); cuad_suma_x:suma_x^2; alpha:((suma_xcuad*suma_y)-(suma_xy*suma_x))/((n*suma_xcuad)-cuad_suma_x), numer; beta:((n*suma_xy)-(suma_x*suma_y))/((n*suma_xcuad)-cuad_suma_x), numer; fx_estimada:alpha+beta*x_;

Lo que nos da la siguiente recta de ajuste (la estimación de la función). $\hat{f(x_{i})}=\alpha+\beta x_{i}=0.1693755346449957+0.8212147134302823x_{i}$ Entonces podemos hacer la representación gráfica del ajuste de los datos:

kill (all); x_:[1,3,4,6,7,8,9,10,11,12]; fx:[1,2,4,5,7,9,2,10,10,10]; x_aproximar:2; fx_estimada:0.8212147134302823*x+0.1693755346449957; fx_estimada_x_aproximar: ev(fx_estimada, x=x_aproximar), numer; plot2d([[discrete, x_, fx], [discrete, [[x_aproximar,fx_estimada_x_aproximar]]],fx_estimada], [x,0,15],[y,0,10], [style, points, points, lines], [color,green, red, orange], [xlabel, «Número de empleados»], [ylabel, «Satisfacción del cliente»], [legend, false]);

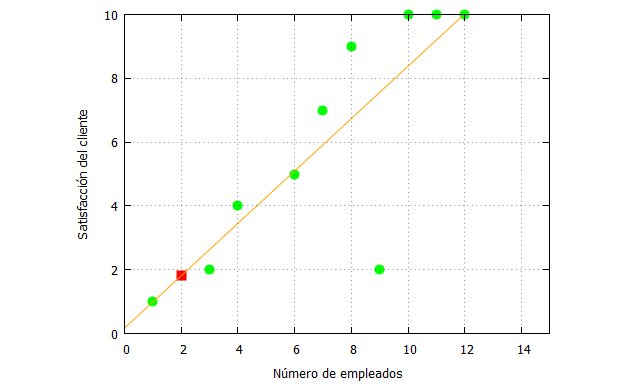
Para 2 empleados la función de ajuste estimada nos dice que la satisfacción será de 1.81.

En próximos posts hablaremos con más detalle de la evaluación de este ajuste, pero ahora simplemente los estudiantes pueden hacer un ejercicio de reflexión ante el visionado de la superposición de las dos funciones computadas, la primera con splines cúbicas y la segunda con el método de los mínimos cuadrados.

load (interpol); p:[[1,1],[3,2],[4,4], [6,5],[7,7],[8,9],[9,2],[10,10],[11,10],[12,10]]; splines: cspline(p); x_:[1,3,4,6,7,8,9,10,11,12]; fx:[1,2,4,5,7,9,2,10,10,10]; x_aproximar:2; x_interpolar:x_aproximar; fx_estimada:0.8212147134302823*x+0.1693755346449957; fx_estimada_x_aproximar: ev(fx_estimada, x=x_aproximar), numer; f_splines: ev(splines,x=x_interpolar), numer; plot2d([[discrete, x_, fx], [discrete, [[x_aproximar,fx_estimada_x_aproximar], [x_interpolar,f_splines]]],fx_estimada,splines], [x,0,15],[y,0,10], [style, points, points, lines, lines], [color, green, red, magenta, orange, magenta], [xlabel, «Número de empleados»], [ylabel, «Satisfacción del cliente»], [legend, false]);

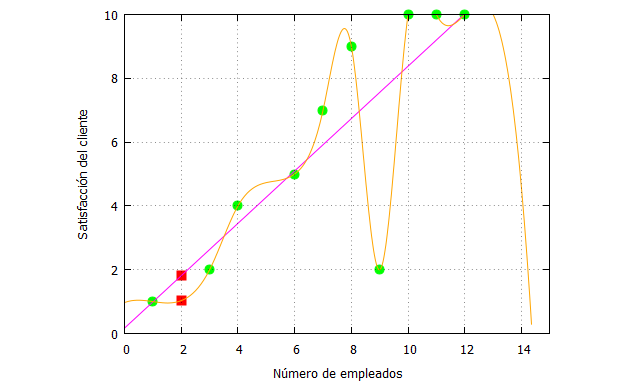
Cuando el número de empleados es 2, la estimación del nivel de satisfacción difiere en función del método empleado. Además, hemos realizado el ajuste de mínimos cuadrados sin tener en cuenta que aparentemente hay una ruptura de la linealidad cuando el número de empleados se incrementa. En posteriores posts, analizaremos con más tranquilidad estos detalles.

Conclusión

Hemos comparado los resultados obtenidos con splines cúbicas con respecto al ajuste de mínimos cuadrados ordinarios, sin entrar en profundidades sobre la idoneidad de ambos análisis. Las predicciones que podemos hacer en base a los datos empíricos divergen, lo que nos debe advertir de lo prudentes que hemos de ser a la hora de analizar los datos.

Category: METODOLOGÍA DE INVESTIGACIÓN

1 comentario en «AJUSTE DE FUNCIONES (I): SPLINES VS MÍNIMOS CUADRADOS»