LA PARADOJA DE CHEVALIER DE MERE

Uno de los objetivos fundamentales de mi labor como profesor de marketing es hacer ver a los estudiantes que necesitan una formación científica muy alta para entender mejor los fenómenos sociales a los que se enfrentan. Por ello, hacemos énfasis en la importancia de las matemáticas, la lógica y la heurística para la toma de decisiones, pero con especial interés en estimular el pensamiento y la formación en estadística.

La paradoja de Chevalier de Mere es una buena forma de mostrar cómo los razonamientos aparentemente lógicos y sencillos pueden ser erróneos, con lo que se necesita de un cierto dominio de herramientas matemáticas para llegar al resultado correcto.

La paradoja

Aris Spanos, uno de los grandes maestros en econometría de nuestros días, en su libro Probability Theory and Statistical Inference, la describe de la siguiente forma:

En el siglo XVII, Pascal envió una carta a Fermat en relación a un problema que le había planteado un noble (y experto jugador) llamado Chevalier de Mere.

De Mere observó la siguiente regularidad derivada de los datos empíricos:

• La probabiliad de obtener al menos un 6 en 4 lanzamientos de un dado es mayor de 0.5
• La probabilidad de obtener al menos un 6 doble (un 12) en 24 lanzamientos de dos datos es menor que 0.5

De Mere se preguntaba cómo eso era posible si, siguiendo un razonamiento aparentemente lógico, ambas probabilidades debían ser iguales, es decir, conseguir un 6 sobre 4 lanzamientos de un dado debería ser lo mismo que conseguir un doble 6 en 24 lanzamientos de 2 dados, ya que 4/6 es igual a 24/36.

La solución

Aris Spanos, sin embargo, argumenta que no existe tal paradoja, porque cuando uno analiza los datos con suficiente rigor, las probabilidades difieren.

• La probabilidad de obtener un doble 6 es:

• La probabilidad de obtener un doble 6 en n lanzamientos es:

 

• La probabilidad de no obtener un doble 6 en n lanzamientos es:

 

• La probabilidad de obtener al menos un doble 6 en n lanzamientos es: 
• Para

 

En el caso de un dado:

• La probabilidad de obtener un  6 es:

 

• La probabilidad de obtener un 6 en m lanzamientos es:

• La probabilidad de no obtener un  6 en m lanzamientos es:

 

• La probabilidad de obtener al menos un 6 en m lanzamientos es: 
• Para 

 

Por tanto, el resultado empírico de de Mere era correcto, pero su razonamiento lógico fallaba.

Una explicación más clara

Podemos obtener una explicación más clara sobre la solución del problema si consultamos el (recomendable) artículo de  Basulto y Camúñez (2007).

No obstante, podemos simplemente proponer un razonamiento que nos lleve a concluir que ambas probabilidades son diferentes.

Podemos reordenar las ecuaciones anteriores de la siguiente forma: Si llamamos: Entonces: Tomando logaritmos neperianos a ambos lados:

Si ahora suponemos que , es decir que ambas probabilidades son iguales, entonces:

De este modo:

Así, la única manera en que las probabilidades pueden ser iguales es cuando se cumple la relación anterior, es decir, que la razón del número de ensayos sea igual a la inversa de la razón de los logaritmos neperianos de las probabilidades de no obtener el número deseado.

Para el caso del ejemplo de Spanos:

lo que es, obviamente, imposible, y por tanto ambas probabilidades no pueden ser iguales.

Para que ambas fueran iguales, entonces para el caso de dos dados la probabilidad de no obtener un doble 6 debería ser 34.926/36 en lugar de 35/36.

También se puede ver de otro modo, y es que si los ensayos son los mismos, por ejemplo 4, entonces: que obviamente no es posible.

Un gráfico que puede ayudar a comprender lo que está sucediendo es el que relaciona la probabilidad de no obtener el número deseado cuando se lanzan k dados:

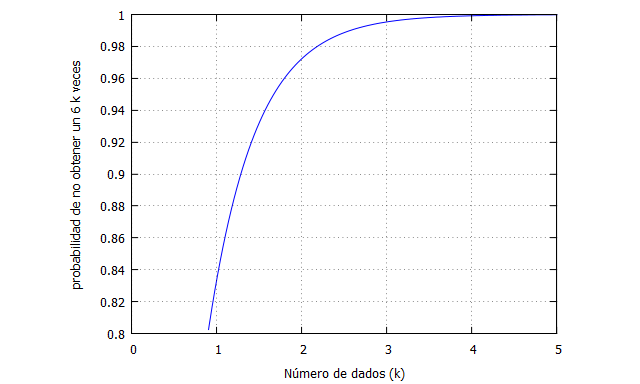
Como se aprecia, el incremento de probabilidad es no lineal (en realidad la figura debería ser dibujada con puntos discretos para k=1, k=2, etc, pero se ha dibujado contínua para que se aprecie mejor la no linealidad).

Conclusión

La paradoja de de Mere no es en realidad una paradoja, sino una muestra de que razonamientos aparentemente sencillos y lógicos no dan el resultado correcto. Para llegar a resolver este tipo de problemas, necesitamos herramientas matemáticas que nos ayuden a no equivocarnos (o a hacerlo lo menos posible).

Los estudiantes de marketing deben apresurarse a interesarse por este sistema de pensamiento para tomar decisiones, sobre todo cuando han de analizar datos empíricos.