Durante los próximos meses vamos a ir comentando algunos de los puntos más destacados de una obra extraordinaria: Probability Theory and Statistical Inference, de Aris Spanos, un libro que debería ser de obligada lectura para todos los estudiantes e investigadores en ciencias.
Lo haremos con el máximo de los respetos, y con el reconocimiento de que la interpretación aquí mostrada no hará justifica al excelso contenido del libro. Sin embargo, la intención es que ayude a estudiantes a introducirse en el mundo de la investigación, así como diseminar los postulados de este gran investigador.
La idea es ir realizando un pequeño post por capítulo, intentando mostrar algunos ejemplos llevados a campos relacionados con mi actividad investigadora.
Capítulo I. Una introducción a la modelización empírica
Spanos define la modelización empírica como una descripción parsimoniosa de fenómenos estocásticos observables, empleando modelos estadísticos.
Un modelo estadístico pretende capturar la información estadística sistemática. Por tanto, es importante ya darnos cuenta que modelizar implica proponer una forma de plantear relaciones entre variables que expliquen cómo se han generado los datos, donde el interés reside en el componente sistemático, es decir, en aquello que está fuera de la aleatoriedad.
Los modelos empíricos envuelven un amplio espectro de procedimientos inter relacionados:
a) Especificación: Elección del modelo estadístico.
b) Estimación: Estimación de los parámetros del modelo.
c) Test de mala especificación: Evaluación de la validez de las asunciones probabilísticas postuladas en el modelo.
d) Re-especificación: Elección alternativa de otro modelo estadístico.
Como muy bien comenta el autor, estas facetas distinguen a los datos observacionales de los experimentales, donde en este último caso el principal objetivo es la estimación, siendo las facetas a) y d) constitutivas del diseño experimental, y donde c) juega un papel más secundario.
Algunas definiciones importantes:
- Fenómeno estocástico: Aquel en que los datos observados exhiben patrones de regularidad inciertos (emplea la palabra “chance”).
- “Chance”: La incertidumbre inherente a la ocurrencia de un determinado resultado.
- Regularidad: Presencia de orden relativo a la ocurrencia de muchos de esos resultados. Es diferente al concepto de aleatoriedad.
Spanos emplea el ejemplo de lanzar dos dados, con el fin de tener una primeración noción intuitiva de conceptos fundamentales.
Vamos a emplear Maxima para dibujar un histograma de este ejemplo:
numeros_2dados:[2, 3, 4, 5, 6, 7, 3, 4, 5, 6, 7, 8, 4, 5, 6, 7, 8, 9, 5, 6, 7, 8, 9, 10, 6, 7, 8, 9, 10, 11, 7, 8, 9, 10, 11, 12]$ histogram ( numeros_2dados, nclasses=11, frequency=density, xlabel="Espacio muestral", ylabel="Densidad de probabilidad", fill_color=green, fill_density=0.5);
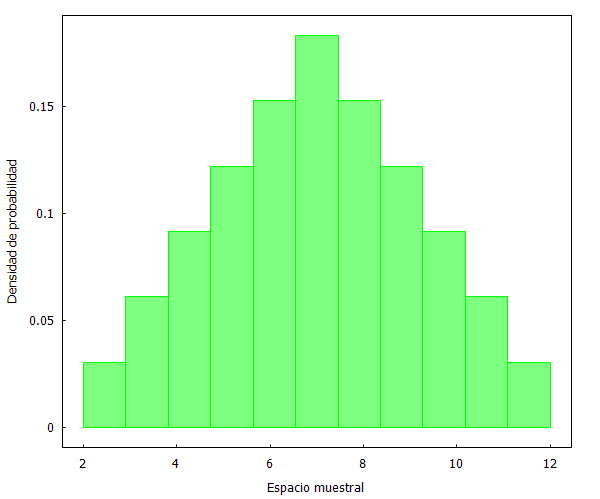
Y ahora de nuevo usamos Maxima para dibujar los resultados de lanzar 2 dados 100 veces, en un gráfico que Spanos denomina “t-plot“:
resultados: makelist(random(11)+2,100); plot2d([[discrete, resultados], [discrete,resultados]], [x,0,100],[y,2,12],[style, points, lines], [color, red, green],[xlabel, "Número de lanzamiento"], [ylabel, "Suma de los 2 dados"], [legend, false]);
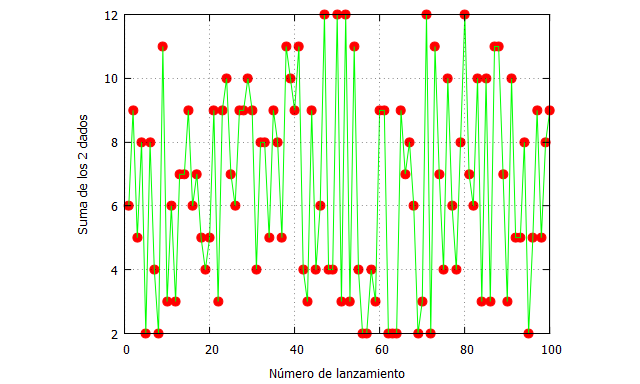
He aquí los 3 conceptos que debemos comprender a la perfección:
[1] Distribución: El histograma desprende una distribución determinada de los datos empíricos, en este caso con mayor concentración en el centro y menos en los extremos.
[2] Independencia: El resultado de un lanzamiento no influye en el siguiente, tal y como muestra el t-plot.
[3] Homogeneidad: Las probabilidades asociadas con los diferentes resultados permanecen idénticas para todos los ensayos realizados.
Veamos un ejemplo práctico con datos reales. Cojamos los 82 partidos jugados por Kemba Walker en la temporada regular de la NBA 2018/19, y realicemos los mismos gráficos:
data:read_matrix(file_search("RUTADELARCHIVO.txt"));
datatranspose:transpose(data);
walker:datatranspose;
histogram (
walker,
nclasses=11,
frequency=density,
xlabel="Espacio muestral",
ylabel="Densidad de probabilidad",
fill_color=green,
fill_density=0.5)
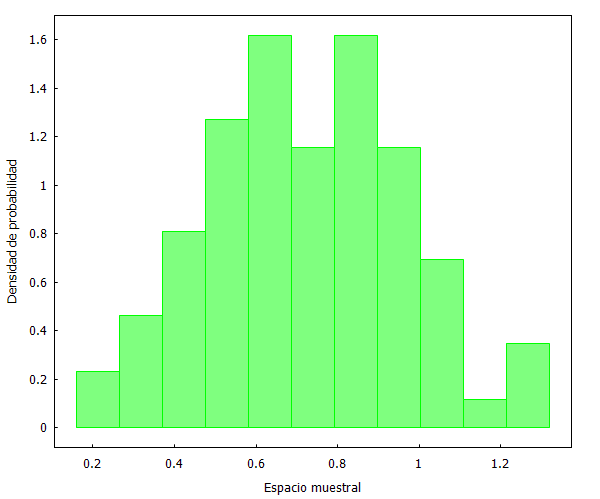
plot2d([[discrete,datatranspose[1]], [discrete,datatranspose[1]]], [x,0,82],[y,0,1.5], [style, points, lines],[color, red, green], [xlabel, "Puntos/minuto"],[ylabel, "Número de partido jugado"], [legend, false]);
Aquí tenemos ya un poco más de dificultad para interpretar los gráficos, aunque disponemos de los 3 mismos conceptos bien representados:
[1] Distribución: Claramente hay una distribución centrada en los valores medios, aunque no con una apariencia tan “Normal” como en un fenómeno aleatorio:
[2] Independencia: No está tan claro que hay total independencia, parece que puede haber la existencia de rachas, de algún componente sistemático que afecte el rendimiento.
[3] Homogeneidad: Tampoco es diáfano que las probabilidades asociadas a los diferentes resultados se mantengan constantes.
Esto es una mera ilustración de que, para cada conjunto de datos que tengamos, necesitamos estudiar detenidamente varios aspectos de los mismos que conformarán nuestras asunciones probabilísticas. Los gráficos son una gran ayuda, pero también habremos de ayudarnos de test que nos asistan cuando, como en el caso de los datos de Kemba Walker, no lo tengamos tan claro.
El siguiente paso es trasladar los patrones de regularidad con incertidumbre en información estadística con un componente sistemático. Para ello, prestemos atención a la siguiente definición:
Un modelo estadístico es un conjunto de asunciones probabilísticas compatibles que provienen de tres categorías: [D] distribución, [M] dependencia, [H] heterogeneidad.
Obviamente, coinciden con las 3 facetas con las que intepretábamos los datos anteriores.
Spanos incide en que la modelización empírica no trata sobre elegir óptimos estimadores, sino sobre escoger modelos estadísticos adecuados. Así, distingue entre la información estadística y la teoría que hay detrás del modelo. De esta forma, la teoría de la probabilidad funciona como un lenguaje neutral independiente de la teoría económica, psicológica, etc., que hay detrás del modelo. La validez del modelo descansa primeramente sobre la validez de las asunciones probabilísticas.
Por ello, este proceso de análisis es deductivo-inductivo, en el sentido en que el razonamiento toma la forma de modus ponens:
si p, entonces q
Si ciertas premsas son asumidas, ciertas conclusiones necesariamente se obtienen. Si las asunciones probabilísticas no se cumplen, se interpreta como que hay un componente sistemático añadido que hay que tener en cuenta, por lo que hay que re-especificar el modelo.
De nuevo enfatiza la distinción entre un modelo estadístico y un modelo teórico; el modelo estadístico es un testigo sin prejuicios acerca de la validez de las asunciones, sobre cuyo testimonio se evalúa la idoneidad empírica del modelo teórico. Así, ninguna teoría, por sosfisticada que sea, puede compensar un modelo estadístico mal especificado.
Spanos introduce la siguiente notación:
- Datos transversales:
donde k, representa individuos, empresas, etc.
- Datos longitudinales:
donde t es el tiempo.
- Datos de panel:
Es importante señalar que los datos transversales no tienen un orden natural temporal, pero sí que lo pueden tener a nivel espacial o de cualquier otra dimensión:
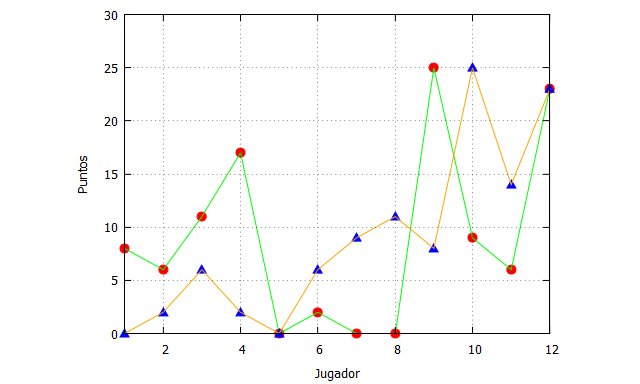
Para mostar esto gráficamente, podemos emplear los puntos obtenidos por los jugadores de los Warriors en el segundo partido de la final de la NBA 2019.
kill (all);
data:read_matrix(file_search("RUTADELARCHIVO.txt"));
datatranspose:transpose(data);
plot2d([[discrete,datatranspose[1]],
[discrete,datatranspose[1]],
[discrete,datatranspose[2]],
[discrete,datatranspose[2]]],
[x,1,12],[y,0,30],
[style, points, lines, points, lines],
[color, red, green, blue, orange],
[xlabel, "Jugador"],[ylabel, "Puntos"],
[legend, false]);
Los puntos rojos y línea verde representan los datos ordenados alfabéticamente, pero los datos con puntos azules y línea naranja lo hacen en función creciente de los minutos jugados. Por tanto, aunque estos datos sean claramente transversales porque se han obtenido como una foto instantánea al terminar el partido, existe un ordenamiento en (al menos) una dimensión.
Seguiremos próximamente con el Capítulo II.
