Continuamos con el tercer capítulo de: Probability Theory and Statistical Inference, de Aris Spanos.
Capítulo III. La noción de un modelo probabilístico
Comencemos con una visión simple del concepto de variable aleatoria.
El autor divide en 3 pasos el objetivo de mapear el espacio probabilístico sobre la recta real
:
Paso 1:
donde se preserva la estructura del espacio de eventos , tal que
para cada
.
Este es el concepto simple de variable aleatoria.
Paso 2:
es una función de probabilidad
es una función de distribución
Paso 3:
es una función de densidad
para todo
Es decir, para cada valor de X, o lo que es lo mismo, para cada , la función de densidad
especifica la probabilidad. Y esto hace que no sea necesario conocer las probabilidades a priori, sino que simplemente estén en función de algún parámetro
.
Así podemos obtener una familia de funciones de densidad determinada por , lo que va a ser esencial para el modelado estadístico. Es decir, en función de las características del experimento se pueden proponer diferentes funciones de densidad con divergentes valores de
.
Lanzar tiros libres en baloncesto
Podemos definir diferentes experimentos sobre el lanzamiento de tiros libres en baloncesto. Por ejemplo:
1) Al lanzar un tiro libre podemos definir la variable aleatoria:
: acertar
Según este experimento podemos definir la distribución de Bernuilli:
2) Al lanzar varios tiros libres, podemos definir la variable aleatoria:
: número de aciertos total en n lanzamientos
Como bien indica Spanos, la repetición de n ensayos de Bernouilli nos da la distribución binomial cuya función de densidad es:
donde:
Tanto el caso 1) como el 2) lo comentamos en el Capítulo IIa.
3) Pero consideremos de nuevo el experimento de lanzar varios tiros libres, pero ahora definamos la siguiente variable aleatoria:
: lanzar tiros libres hasta anotar
Ahora la elección de la función de densidad ya no es la de una distribución binomial, sino geométrica:
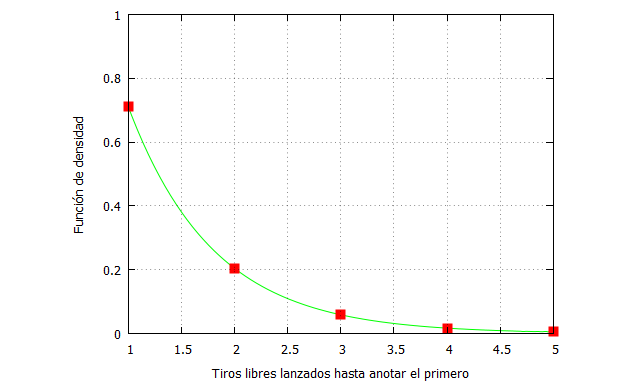
Si seguimos con el ejemplo de Luka Doncic y su 71.3% de efectividad en los lanzamientos libres en 2018/19, entonces:
que obviamente coincide con su probabilidad, es decir, que cuando lanza un sólo tiro libre el valor es el de la probabilidad de anotar. Pero. ¿cuál sería la probabilidad de que tuviera que lanzar 3 tiros libres para anotar? O lo que es lo mismo, que fallara los dos primeros y anotara el tercero:
Es decir, que un poco más del 5% de las ocasiones en las que Doncic lance tres tiros libres seguidos, fallará los dos primeros y anotará el tercero.
En el siguiente código de Maxima se especifica la distribución geométrica para n=5, con las probabilidades correspondientes:
kill (all);
tiroslibres(n,x,fi):=fi*(1-fi)^(x-1);
funcion(x):=tiroslibres(5,x,0.713);
unlanzamiento:funcion(1);
doslanzamientos:funcion(2);
treslanzamientos:funcion(3);
cuatrolanzamientos:funcion(4);
cincolanzamientos:funcion(5);
plot2d([funcion(x),[discrete,[[1,unlanzamiento],
[2,doslanzamientos],[3,treslanzamientos],
[4,cuatrolanzamientos], [5,cincolanzamientos]]]], [x,1,5],
[y,0,1], [style, lines, points],[color, green, red],
[xlabel, "Tiros libres lanzados hasta anotar el primero"],
[ylabel, "Función de densidad"], [legend, false]);

En el siguiente post, avanzaremos con una noción más general de variable aleatoria.
