TEORÍA DE PROBABILIDAD E INFERENCIA ESTADÍSTICA SEGÚN ARIS SPANOS (IIIc)

Continuamos con el tercer apartado del tercer capítulo de Probability Theory and Statistical Inference, de Aris Spanos.

Si vemos $P_{X}(.)$ como sólo una función del punto final del intervalo $(-\infty,x]$ , entonces podemos definir la distribución acumulada (cdf):

$F_{X}(.): \mathbb{R}\rightarrow [0,1], F_{X}(x)=\mathbb{P}\left \{s:X(s)\leqslant x \right \}=P_{X}((-\infty ,x)])$

Ahora sí hemos generado una función que relaciona el número real asignado a cada posible evento con su probabilidad de ocurrencia. Pero en este caso es la probabilidad acumulada.

Para el caso simple (discreto) tenemos la función de densidad:

$f_{x}(.): \mathbb{R}\rightarrow [0,1], f_{x}(x)=\mathbb{P}(X=x),x\in\mathbb{R}_{X}$

Por tanto, los espacios probabilísticos pueden simplificarse en el caso de variables aleatorias discretas y continuas a los siguientes:

$\left ( S,\Im,\mathbb{P(.)} \right )\overset{X(.)}{\rightarrow}(\mathbb{R},f_{x}(.))$

$\left ( S,\Im,\mathbb{P(.)} \right )\overset{X(.)}{\rightarrow}(\mathbb{R},F_{X}(.))$

Spanos se plantea en este punto si se pueden definir funciones de densidad para variables continuas y funciones de distribución para variables discretas, y la respuesta es que sí.

$F_{X}(x)=\int_{-\infty }^{x}f_{x}(u)du, f_{x}(u)\geq 0$

$\int_{a }^{b}f_{x}(u)du=F_{x}(b)-F_{x}(a)$

La estatura de los jugadores de la NBA se puede considerar como una variable continua. Desde el inicio de la NBA hasta el año 2015, hay 3984 jugadores cuya estatura se muestra en este archivo.

El histograma de la distribución es el siguiente:

data:read_list(file_search("RUTADELARCHIVO.txt "));
datatranspose:transpose(data);
estatura:datatranspose;
histogram (
estatura,
nclasses=15,
frequency=density,
xlabel="Espacio muestral. Estatura jugadores NBA (cm)",
ylabel="Densidad de probabilidad",
fill_color=green,
fill_density=0.5);

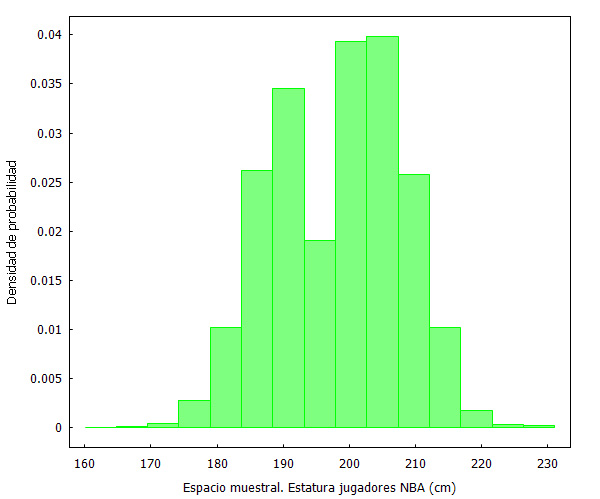
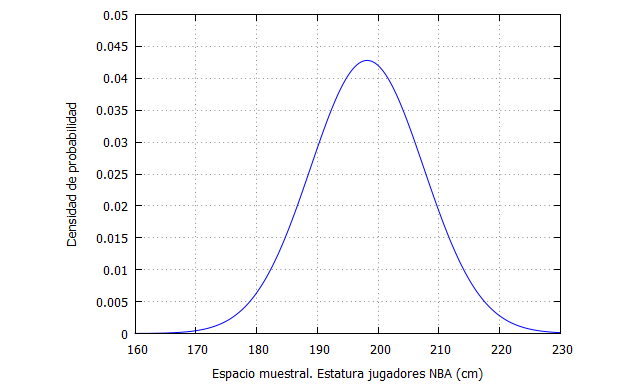
Es una distribución que se aproxima a una Normal, pero que no sabemos realmente si lo es. Recordemos que una distribución Normal tiene como función de densidad:

$f_{x}(x;\theta )=\frac{1}{\sigma \sqrt{2\pi }}e^{ -\frac{(x-\mu )^{2}}{2\sigma ^{2}}},\theta:=(\mu,\sigma ^{2})\in \mathbb{R}\times \mathbb{R}_{+},x\in \mathbb{R}$

De este modo, podemos tomar como media y desviación típica la de la muestra, como una estimación de los parámetros poblacionales.

$f_{x}(x;\theta )=\frac{1}{9.3\sqrt{2\pi }}e^{ -\frac{(x-198.2 )^{2}}{2\cdot 9.3 ^{2}}},\theta:=(198.2,9.3 ^{2})\in \mathbb{R}\times \mathbb{R}_{+},x\in \mathbb{R}$

El resultado, tras emplear Stata 13.0, es el mostrado en el gráfico siguiente:

Sin embargo, otras distribuciones también podrían ajustarse a los datos. Por ejemplo, la distribución Weibull:

$f_{x}(x;\theta )=\frac{\beta x^{\beta -1}}{\alpha ^{\beta }}e^{ -\frac{(x-\mu )^{\beta }}{\alpha }},\theta:=(\alpha,\beta)\in \mathbb{R}_{+}^{2},x> \mu \in \mathbb{R}$

También la distribución logística podría ajustarse aproximadamente bien a los datos:

$f_{x}(x;\theta )=\frac{e^{-(x-m)/b)}}{b[1+e^{-(x-m)/b)}]^{2}},\theta:=m,b\in \mathbb{R}_{+}^{2},x\in \mathbb{R}$

En Maxima podemos representar las 3 distribuciones, Normal, Weibull y logística, de la siguiente forma:

load(distrib);
plot2d([pdf_weibull(x,18,198.2),pdf_logistic(x,198.2,5.5),
pdf_normal (x, 198.2, 9.32)], 
[x,160,230],[y,0,0.05],
[xlabel, "Espacio muestral. Estatura jugadores NBA (cm)"],
[ylabel, "Densidad de probabilidad"], 
[legend, "Weibull", "Logistica", "Normal"]);

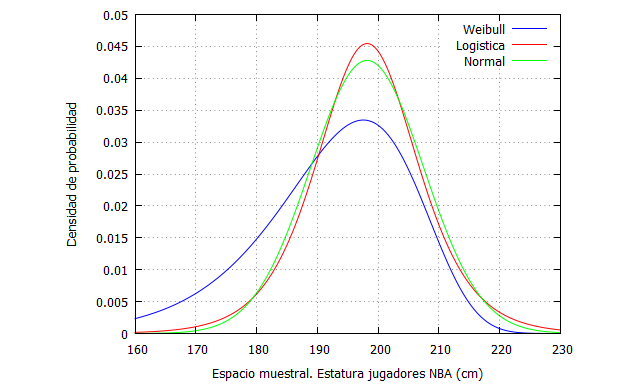
Las 3 distribuciones consideradas, estipulan que $x\in \mathbb{R}$ . Esto es un elemento a tener en cuenta porque en este caso tenemos una distribución de estatura cuyos valores no pueden ser nunca cero o menor que cero. Por tanto, $x\in \mathbb{R}_{+}$ . Desde el punto de vista práctico quizá para este ejemplo no tenga demasiada importancia, pero a nivel didáctico nos sirve para justifica la búsqueda de otra función de densidad que sólo permita valores positivos.

Una opción es emplear la función chi-cuadrado:

$f_{x}(x;\theta )=\frac{x^{(r/2)-1}e^{-x/2}}{\Gamma(r/2)2^{r/2} },\theta:=(r)\in \mathbb{R}_{+},x>0 \in \mathbb{R}$

donde r son los grados de libertad y $\Gamma$ es la función Gamma.

Así, para r=198, y con la ayuda de Stata 13.0, vemos la distribución chi-cuadrado en azul.

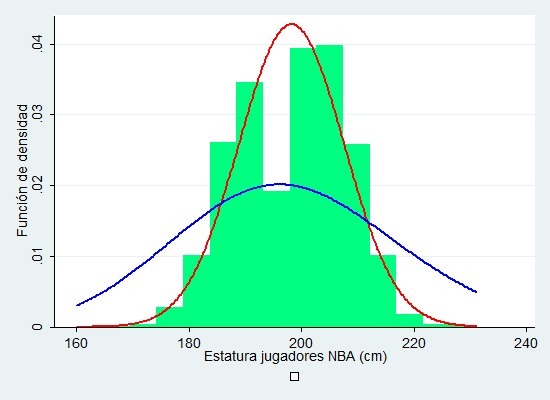
Como se puede apreciar, el ajuste no es tan bueno como la distribución Normal, aunque pese a que la Normal tenga un rango de valores teórico fuera del permitido por este caso.

En definitiva, hemos visto que podemos simplificar los espacios probabilísticos empleando funciones de densidad y de distribución. Así, con la adecuada elección de la función de densidad podemos relacionar los eventos con su probabilidad de ocurrencia, teniendo en cuenta que en distribuciones continuas lo pertinente es analizar la probabilidad entre 2 puntos de la distribución.

Category: METODOLOGÍA DE INVESTIGACIÓN